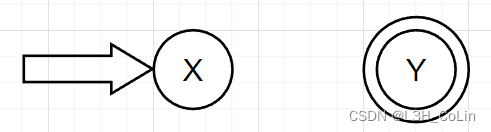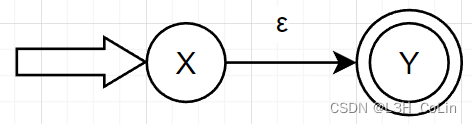词法分析程序用于将输入的字符转化为单词符号,之后与语法分析器进行互动,逐词输入到语法分析器中用于语法分析器进行语法分析。
语言的单词符号指语言中具有独立意义的最小语法单位,即单词符号是程序语言的基本语法单位。程序语言的单词符号一般可以分为下面5种:
关键字:表示语义的词语,如if、while等
标识符:各种名字,如变量名、常量名等
常数:整数、小数、布尔型等
运算符:加减乘除
界符:分号、括号等
通常表示为二元式:(单词种别,单词自身的值) 。单词种别指单词的种类,通常给一个单词对应一个整数码 ,目的是最大限度地把各个单词区别开。单词自身的值是编译中其他阶段需要的信息,如果一个种别只对应一个单词符号,那么这个单词的种类编码就能够完全代表其自身的值,如if关键字只需要一个种别码就可以知道读取到了if,而不需要额外指定值。如果一个种别对应多个单词符号,则需要给出单词自身的值。如定义整数的种类对应的编码为10,则词法分析程序遇到整数5时则会记录一个二元式:(10, 5)。
正规式实际上类似于多种编程语言中都在使用的正则表达式。其正式定义采用递归定义的形式:设有字母表Σ = a 1 , a 2 , … , a n Σ={a1, a2,…, an} Σ = a 1 , a 2 , … , a n Σ Σ Σ
Φ Φ Φ Σ Σ Σ Φ Φ Φ { } \{\} { }
ε ε ε Σ Σ Σ { ε } \{ε\} { ε }
a i a_i a i Σ Σ Σ a i a_i a i { a i } \{a_i\} { a i }
如果e 1 e_1 e 1 e 2 e_2 e 2 Σ Σ Σ L ( e 1 ) L(e_1) L ( e 1 ) L ( e 2 ) L(e_2) L ( e 2 )
(1) e 1 ∣ e 2 e_1|e_2 e 1 ∣ e 2 Σ Σ Σ L ( e 1 ∣ e 2 ) = L ( e 1 ) ∪ L ( e 2 ) L(e_1|e_2)=L(e_1)∪L(e_2) L ( e 1 ∣ e 2 ) = L ( e 1 ) ∪ L ( e 2 )
(2) e 1 e 2 e_1e_2 e 1 e 2 Σ Σ Σ L ( e 1 e 2 ) = L ( e 1 ) L ( e 2 ) L(e_1e_2)=L(e_1)L(e_2) L ( e 1 e 2 ) = L ( e 1 ) L ( e 2 )
(3) ( e 1 ) ∗ (e_1)^* ( e 1 ) ∗ Σ Σ Σ L ( ( e 1 ) ∗ ) = ( L ( e 1 ) ) ∗ L((e_1)^*)=(L(e_1))^* L ( ( e 1 ) ∗ ) = ( L ( e 1 ) ) ∗
注意:虽然( a ∣ b ) ∗ (a|b)^* ( a ∣ b ) ∗ { a , b } ∗ \{a,b\}^* { a , b } ∗ { a , b } ∗ \{a,b\}^* { a , b } ∗ 这句话说的很容易让人误解,它指的是不是所有的子集都是正规集。如{ a n b n ∣ n ≥ 1 } \{a^nb^n|n\ge 1\} { a n b n ∣ n ≥ 1 } 凡是不能使用正规文法表示的符号串集合都不能被称为正规集。
如果两个正规式描述的正规集相同,称这两个正规式等价,可以使用等号连接。
正规式的性质:令A , B 和 C 均为正规式,则
A ∣ B = B ∣ A A | B = B | A A ∣ B = B ∣ A A ∣ ( B ∣ C ) = ( A ∣ B ) ∣ C A | ( B | C) = (A | B) | C A ∣ ( B ∣ C ) = ( A ∣ B ) ∣ C A ( B C ) = ( A B ) C A(BC) = (AB)C A ( B C ) = ( A B ) C A ( B ∣ C ) = A B ∣ A C A(B | C) = AB | AC A ( B ∣ C ) = A B ∣ A C ( A ∣ B ) C = A C ∣ B C (A | B)C = AC | BC ( A ∣ B ) C = A C ∣ B C A ε ∣ ε A = A Aε | εA = A A ε ∣ ε A = A A ∗ = A A ∗ ∣ ε = A ∣ A ∗ = ( A ∣ ε ) ∗ A^* = AA^* | ε = A | A^* = (A | ε )^* A ∗ = A A ∗ ∣ ε = A ∣ A ∗ = ( A ∣ ε ) ∗ ( A ∗ ) ∗ = A ∗ (A^* )^* = A^* ( A ∗ ) ∗ = A ∗
正规文法与正规式之间可以进行转换。
固定方法:
将正规文法中的每一个非终结符表示成关于它的一个正规式方程,获得一个联立方程组。
按照求解规则:
若x = α x ∣ β x=\alpha x|\beta x = α x ∣ β x = α ∗ β x=\alpha^*\beta x = α ∗ β 若x = x α ∣ β x=x\alpha|\beta x = x α ∣ β x = β α ∗ x=\beta\alpha^* x = β α ∗
固定方法:
令V T = Σ V_T=\Sigma V T = Σ
对任意正规式R R R Z Z Z Z → R Z\rightarrow R Z → R S = Z S=Z S = Z
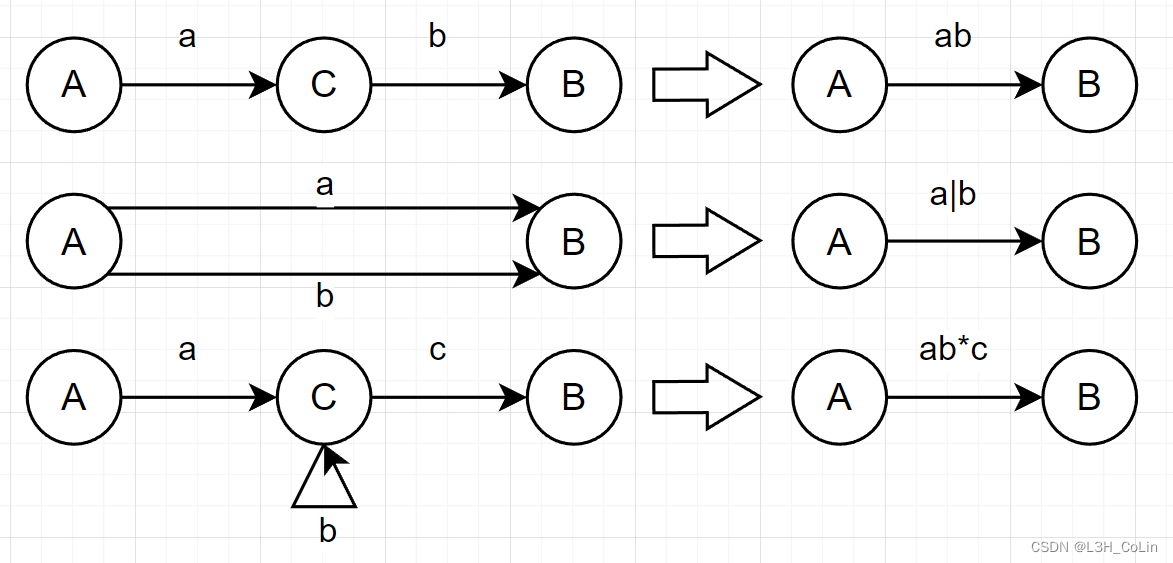
若a a a b b b A → a b A\rightarrow ab A → a b A → a B A\rightarrow aB A → a B B → b B\rightarrow b B → b B B B
在已经转换的文法中,将形如A → a ∗ b A\rightarrow a^*b A → a ∗ b A → a A ∣ b A\rightarrow aA|b A → a A ∣ b
不断使用规则3和4进行转换直到每一条规则最多含有一个非终结符为止。
有穷自动机是具有离散输入和离散输出系统的一种抽象数学模型。
确定有穷自动机M M M 五元组M = ( Q , Σ , f , S , Z ) M=(Q,\Sigma,f,S,Z) M = ( Q , Σ , f , S , Z ) ,其中
Q Q Q Σ Σ Σ f f f Q × Σ Q×Σ Q × Σ Q Q Q f ( q i , a ) = q j f(q_i,a)=q_j f ( q i , a ) = q j q i q_i q i a a a q j q_j q j q j q_j q j q i q_i q i S S S S ∈ Q S∈Q S ∈ Q Z Z Z Z ⊆ Q Z⊆Q Z ⊆ Q
一个DFA可以使用矩阵表示,行表示状态,列表示输入符号,矩阵元素表示f ( q , a ) f(q,a) f ( q , a ) 状态转换矩阵或转换表 。一个DFA也可以表示为一个状态转换图。对于Σ ∗ \Sigma^* Σ ∗ β \beta β β \beta β β \beta β M M M 所接受 。DFA所识别的符号串的全体记为L ( M ) L(M) L ( M ) DFA M M M 。
NFA与DFA不同之处在f f f S S S S ⊂ Q S\subset Q S ⊂ Q
对于任意一个NFA M M M M ′ M' M ′ L ( M ) = L ( M ′ ) L(M)=L(M') L ( M ) = L ( M ′ )
方法如下:
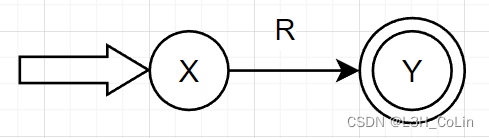
首先引进初始结点X和终止结点Y,将R表示为拓广转换图:
分析R R R R R R
若R = ∅ R=\empty R = ∅
若R = ε R=\varepsilon R = ε
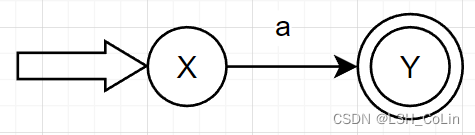
若R = a ( a ∈ Σ ) R=a(a\in\Sigma) R = a ( a ∈ Σ )
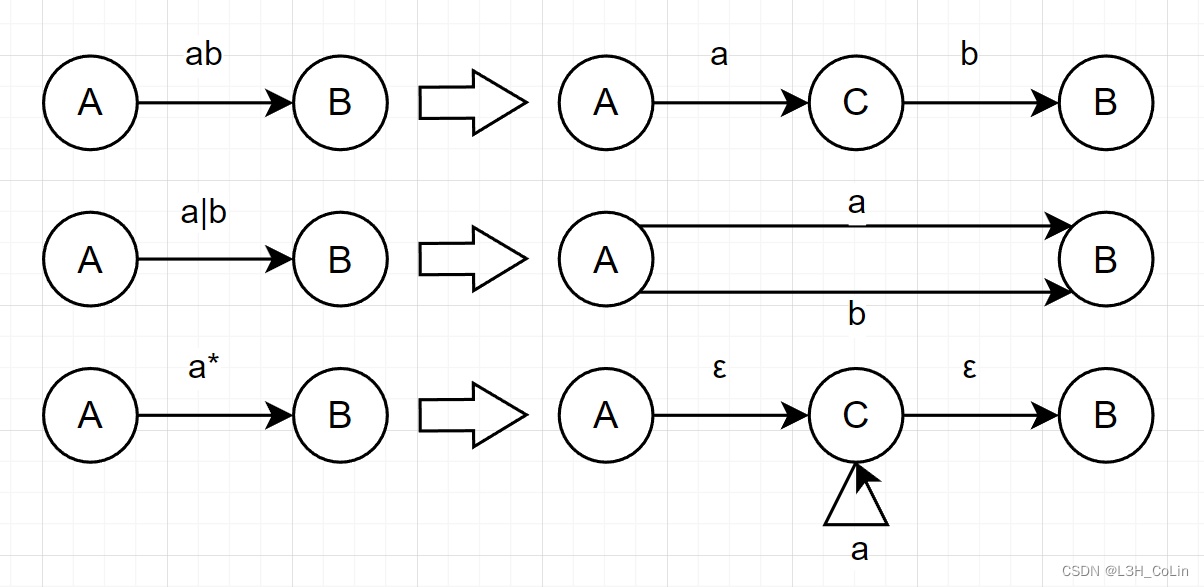
若R R R ε ε ε
整个分裂过程中,所有新结点均采用不同名字,保留X和Y为全图唯一初态结点和终态结点。
ε \varepsilon ε ε-CLOSURE ( I ) \operatorname{\varepsilon-CLOSURE}(I) ε - C L O S U R E ( I ) 设I I I N N N ε-CLOSURE ( I ) \operatorname{\varepsilon-CLOSURE}(I) ε - C L O S U R E ( I )
若s ∈ I s\in I s ∈ I s ∈ ε-CLOSURE ( I ) s\in\operatorname{\varepsilon-CLOSURE}(I) s ∈ ε - C L O S U R E ( I )
若s ∈ I s\in I s ∈ I ε \varepsilon ε s ′ s' s ′ ε-CLOSURE ( I ) \operatorname{\varepsilon-CLOSURE}(I) ε - C L O S U R E ( I )
即I I I ε \varepsilon ε
NFA N N N M M M
置DFA M M M Q ′ Q' Q ′ Z ′ Z' Z ′
给出M M M S ′ = ε-CLOSURE ( ∣ S ∣ ) S'=\operatorname{\varepsilon-CLOSURE}(|S|) S ′ = ε - C L O S U R E ( ∣ S ∣ ) S ′ S' S ′ Q ′ Q' Q ′
如果Q ′ Q' Q ′ T = { q 1 , . . . , q n } , q i ∈ Q T=\{q_1,...,q_n\},q_i\in Q T = { q 1 , . . . , q n } , q i ∈ Q f ′ ( T , a ) f'(T,a) f ′ ( T , a )
对于每一个a ∈ Σ a\in\Sigma a ∈ Σ J = f ( { q 1 , . . . , q n } , a ) = f ( q 1 , a ) ∪ . . . ∪ f ( q n , a ) , U = ε-CLOSURE ( J ) J=f(\{q_1,...,q_n\},a)=f(q_1,a)\cup...\cup f(q_n,a),U=\operatorname{\varepsilon-CLOSURE}(J) J = f ( { q 1 , . . . , q n } , a ) = f ( q 1 , a ) ∪ . . . ∪ f ( q n , a ) , U = ε - C L O S U R E ( J ) U U U Q ′ Q' Q ′ U U U Q ′ Q' Q ′ f ′ ( T , a ) = U f'(T,a)=U f ′ ( T , a ) = U M M M U U U N N N U U U M M M Z ′ Z' Z ′
对T T T T T T
重复步骤3直到Q ′ Q' Q ′
重新命名Q ′ Q' Q ′ M M M
说人话:就是根据闭包确定原NFA的结点集合应该如何划分(注意这些集合可能会有重叠),首先求起始点的闭包,然后看闭包中的元素接收某一个符号a a a
DFA的化简的目标是找到一个状态数量更少的等价的DFA。化简后DFA中没有多余状态,状态集中没有两个状态是相互等价的。
有穷自动机的多余状态 指无论如何也无法到达的状态。
等价状态 指在有穷自动机中两个状态s , t s,t s , t s , t s,t s , t { Q , Σ , f , S 0 , F } \{Q,\Sigma,f,S_0,F\} { Q , Σ , f , S 0 , F } ∀ α ∈ Σ ∗ , f ( s , α ) ∈ F ⇔ f ( t , α ) ∈ F \forall\alpha\in\Sigma^*,f(s,\alpha)\in F\Leftrightarrow f(t,\alpha)\in F ∀ α ∈ Σ ∗ , f ( s , α ) ∈ F ⇔ f ( t , α ) ∈ F
化简算法 :
将DFA M M M Q Q Q F F F ¬ F \lnot F ¬ F Π \Pi Π
对Π \Pi Π Π n e w \Pi_{new} Π n e w Π \Pi Π G G G
将G G G G G G s , t s,t s , t a a a s , t s,t s , t Π \Pi Π
用G G G G G G Π n e w \Pi_{new} Π n e w
如果Π n e w = Π \Pi_{new}=\Pi Π n e w = Π Π = Π n e w \Pi=\Pi_{new} Π = Π n e w
分划结束后对分划中每一个子集选出一个状态为代表,删去其他所有等价状态,并将指向其他状态的箭头改为指向这个代表状态。算法结束。
说人话:首先把终态集和非终态集分开,然后一个集合一个集合验证,如果这个集合中所有状态对于一个相同的输入都能到达相同的集合,那么这个集合中所有元素都等价;如果不能,那么看哪些到达这个集合,哪些到达那个集合,按照到达的集合来对这个集合进行划分。重复上面的操作直到没有办法划分为止。最终每一个划分只留一个状态,调整一下箭头走向。算法结束。
也就是从正规式到有穷自动机转换的逆过程,是一个去结点合并表达式的过程。
对于右线性正规文法G = ( V N , V T , P , S ) G=(V_N,V_T,P,S) G = ( V N , V T , P , S ) M = ( Q , Σ , f , q 0 , Z ) M=(Q,\Sigma,f,q_0,Z) M = ( Q , Σ , f , q 0 , Z )
将V N V_N V N M M M D D D D ∉ V N D\notin V_N D ∈ / V N Q = V N ∪ { D } , Z = { D } , Σ = V T , q 0 = S Q=V_N\cup\{D\},Z=\{D\},\Sigma=V_T,q_0=S Q = V N ∪ { D } , Z = { D } , Σ = V T , q 0 = S
对于G G G A → a B A\rightarrow aB A → a B ( A , B ∈ V N , a ∈ V T ∪ { ε } ) (A,B\in V_N,a\in V_T\cup\{\varepsilon\}) ( A , B ∈ V N , a ∈ V T ∪ { ε } ) f ( A , a ) = B f(A,a)=B f ( A , a ) = B
对于G G G A → a A\rightarrow a A → a ( A ∈ V N , a ∈ V T ) (A\in V_N,a\in V_T) ( A ∈ V N , a ∈ V T ) f ( A , a ) = D f(A,a)=D f ( A , a ) = D
对于G G G A → ε A\rightarrow\varepsilon A → ε ( A ∈ V N ) (A\in V_N) ( A ∈ V N ) A A A f ( A , ε ) = D f(A,\varepsilon)=D f ( A , ε ) = D
按照上述方法可以构造一个右线性正规文法的NFA,能够识别这个文法的语言。
说人话:将文法中所有非终结符看成一个状态,如果规则右部有非终结符,就从规则左部画箭头标右部的终结符指向右部的非终结符。如果规则右部没有非终结符,就从规则左部画箭头标右部的终结符指向终结状态,这个终结状态不在非终结符中,是另外创建的唯一一个状态。如果规则右部是空字符,可以让规则左部非终结符变成终态或指一个空字符的箭头到终态。
对于左线性正规文法G = ( V N , V T , P , S ) G=(V_N,V_T,P,S) G = ( V N , V T , P , S ) M = ( Q , Σ , f , q 0 , Z ) M=(Q,\Sigma,f,q_0,Z) M = ( Q , Σ , f , q 0 , Z )
将V N V_N V N M M M q 0 q_0 q 0 q 0 ∉ V N q_0\notin V_N q 0 ∈ / V N Q = V N ∪ { q 0 } , Z = { S } , Σ = V T Q=V_N\cup\{q_0\},Z=\{S\},\Sigma=V_T Q = V N ∪ { q 0 } , Z = { S } , Σ = V T
对于G G G A → B a A\rightarrow Ba A → B a ( A , B ∈ V N , a ∈ V T ∪ { ε } ) (A,B\in V_N,a\in V_T\cup\{\varepsilon\}) ( A , B ∈ V N , a ∈ V T ∪ { ε } ) f ( B , a ) = A f(B,a)=A f ( B , a ) = A
对于G G G A → a A\rightarrow a A → a ( A ∈ V N , a ∈ V T ) (A\in V_N,a\in V_T) ( A ∈ V N , a ∈ V T ) f ( q 0 , a ) = A f(q_0,a)=A f ( q 0 , a ) = A
说人话:将文法中所有非终结符看成一个状态,文法开始符号是终态。如果规则右部有非终结符,就从规则右部非终结符画箭头标右部的终结符指向左部。如果规则右部没有非终结符,就从初始状态画箭头标右部的终结符指向规则左部,这个初始状态不在非终结符中,是另外创建的唯一一个状态。箭头指向和右线性文法到有穷自动机是反着来的。
对于有穷自动机M = ( Q , Σ , f , q 0 , Z ) M=(Q,\Sigma,f,q_0,Z) M = ( Q , Σ , f , q 0 , Z ) G = ( V N , V T , P , S ) G=(V_N,V_T,P,S) G = ( V N , V T , P , S )
V N = Q , V T = Σ , S = q 0 V_N=Q,V_T=\Sigma,S=q_0 V N = Q , V T = Σ , S = q 0 若f ( A , a ) = B f(A,a)=B f ( A , a ) = B B ∉ Z B\notin Z B ∈ / Z A → a B A\rightarrow aB A → a B P P P
若f ( A , a ) = B f(A,a)=B f ( A , a ) = B B ∈ Z B\in Z B ∈ Z A → a B ∣ a A\rightarrow aB|a A → a B ∣ a A → a B A\rightarrow aB A → a B B → ε B\rightarrow\varepsilon B → ε P P P
若文法的开始符号S S S S → ε S\rightarrow\varepsilon S → ε P P P
上述只考虑了右线性正规文法,因为构造为右线性正规文法符合我们的习惯,容易理解不易出错。
说人话:右线性正规文法到有穷自动机反着来。
这部分与实验有关,极其重要!需要掌握Flex词法分析程序的原理。
将所有用户不得用作标识符的关键字定义为一类特殊的标识符来处理,并将它们事先安排在一个表格之中,称为关键字表 。利用状态转换图识别一个标识符时需要查询关键字表中是否有这个标识符。
关键字、标识符与常数之间如果没有确定运算符作为界符分隔,则必须需要至少一个空白符作为填充。此时这里的空白符就有了意义。
ch:字符变量保存当前读入的源程序字符
token:字符数组,保存当前单词符号的字符串
getch():读一个字符,函数将缓冲区中读入源程序的下一个字符放在ch中,并更新读指针
getbc():读空白符,每一次调用检查ch中字符是否是空白符,如果是则反复调用getbc()直到遇到一个非空白字符为止。
concat():拼接函数,将当前读取的字符与token相连接。
letter(ch):检查ch中字符是否为字母
digit(ch):检查ch中字符是否为数字
reserve():返回当前保存的token的种别编码,标识符的种别码为10。该函数会查询关键字表。
retract():读字符指针回退一个字符
return():收集并携带必要信息返回调用程序,返回语法分析程序
dtb()+进制转换函数:将token中的字符串转换为数字并返回
1 2 3 4 5 6 7 8 9 /* 预定义段 */ %{ /* 在此添加头文件包含 */ %} /* 在此添加正规式,定义正规式 */ %% /* 规则段 */ %% /* 用户子程序段,定义main函数等函数 */
示例:(编译原理实验lab-1,task-2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 %{ //Add a head file here %} DIGIT [0-9] // 使用DIGIT定义数字,避免下面重复书写 ID [a-z][a-z0-9]* // 标识符 %% {DIGIT}+ {printf( "An integer: %s (%d)\n", yytext,atoi( yytext ) );} {DIGIT}+"."{DIGIT}? {printf( "A float: %s (%g)\n", yytext,atof( yytext ) ); } if|then|begin|end|procedure|function {printf( "A keyword: %s\n", yytext );} {ID} printf( "An identifier: %s\n", yytext ); "+"|"-"|"*"|"/" printf( "An operator: %s\n", yytext ); "{"[^}\n]*"}" /* eat up one-line comments */ [ \t\n]+ /* eat up whitespace */ . printf( "Unrecognized character: %s\n", yytext ); %% int main( argc, argv ) int argc; char **argv; { ++argv, --argc; /* skip over program name */ if ( argc > 0 ) yyin = fopen( argv[0], "r" ); else yyin = stdin; yylex(); }
注意:
规则段中越靠上的规则优先级越大,如上面例子中一众关键字就放在ID的上面一行,是因为它们需要首先进行处理,能够决定整个程序的语法结构。
规则定义部分上方的正规式定义部分互相不存在优先级,也与定义的先后无关。但正规式的匹配采用贪心的策略,即尽量多地进行匹配,如果两个正规式的匹配长度相同,则选择定义靠前的那一个 。
下面是更加全面的例子:(编译原理试验lab-1,task-4)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 /* PL词法分析器 */ /* 功能:能够识别出PL支持的所有单词符号并给出种别值 */ /* 说明:在下面的begin和end之间添加代码,已经实现了标识符和整常量的识别,你需要完成剩下的部分,加油吧! */ /* 提示:因为是顺序匹配,即从上至下依次匹配规则,所以需要合理安排顺序~ */ %{ #include <stdio.h> %} /*** begin ****/ INTCON [\-]?[1-9][0-9]*|0 IDENT [A-Za-z][A-Za-z0-9]* CHARCON '([^\']|\n)*' PLUS \+ MINUS - TIMES \* DIVSYM \/ EQL = NEQ <> LSS < LEQ <= GTR > GEQ >= OFSYM of ARRAYSYM array PROGRAMSYM program MODSYM mod ANDSYM and ORSYM or NOTSYM not LBRACK \[ RBRACK \] LPAREN \( RPAREN \) COMMA , SEMICOLON ; PERIOD \. BECOME := COLON : BEGINSYM begin ENDSYM end IFSYM if THENSYM then ELSESYM else WHILESYM while DOSYM do CALLSYM call CONSTSYM const TYPESYM type VARSYM var PROCSYM procedure %% {OFSYM} {printf("%s: OFSYM\n", yytext);} {ARRAYSYM} {printf("%s: ARRAYSYM\n", yytext);} {PROGRAMSYM} {printf("%s: PROGRAMSYM\n", yytext);} {MODSYM} {printf("%s: MODSYM\n", yytext);} {ANDSYM} {printf("%s: ANDSYM\n", yytext);} {ORSYM} {printf("%s: ORSYM\n", yytext);} {NOTSYM} {printf("%s: NOTSYM\n", yytext);} {BEGINSYM} {printf("%s: BEGINSYM\n", yytext);} {ENDSYM} {printf("%s: ENDSYM\n", yytext);} {IFSYM} {printf("%s: IFSYM\n", yytext);} {THENSYM} {printf("%s: THENSYM\n", yytext);} {ELSESYM} {printf("%s: ELSESYM\n", yytext);} {WHILESYM} {printf("%s: WHILESYM\n", yytext);} {DOSYM} {printf("%s: DOSYM\n", yytext);} {CALLSYM} {printf("%s: CALLSYM\n", yytext);} {CONSTSYM} {printf("%s: CONSTSYM\n", yytext);} {TYPESYM} {printf("%s: TYPESYM\n", yytext);} {VARSYM} {printf("%s: VARSYM\n", yytext);} {PROCSYM} {printf("%s: PROCSYM\n", yytext);} {INTCON} {printf("%s: INTCON\n", yytext);} {CHARCON} {printf("%s: CHARCON\n", yytext);} {IDENT} {printf("%s: IDENT\n", yytext);} {PLUS} {printf("%s: PLUS\n", yytext);} {MINUS} {printf("%s: MINUS\n", yytext);} {TIMES} {printf("%s: TIMES\n", yytext);} {DIVSYM} {printf("%s: DIVSYM\n", yytext);} {EQL} {printf("%s: EQL\n", yytext);} {NEQ} {printf("%s: NEQ\n", yytext);} {LSS} {printf("%s: LSS\n", yytext);} {LEQ} {printf("%s: LEQ\n", yytext);} {GTR} {printf("%s: GTR\n", yytext);} {GEQ} {printf("%s: GEQ\n", yytext);} {LBRACK} {printf("%s: LBRACK\n", yytext);} {RBRACK} {printf("%s: RBRACK\n", yytext);} {LPAREN} {printf("%s: LPAREN\n", yytext);} {RPAREN} {printf("%s: RPAREN\n", yytext);} {COMMA} {printf("%s: COMMA\n", yytext);} {SEMICOLON} {printf("%s: SEMICOLON\n", yytext);} {PERIOD} {printf("%s: PERIOD\n", yytext);} {BECOME} {printf("%s: BECOME\n", yytext);} {COLON} {printf("%s: COLON\n", yytext);} [ \n\t]+ {} . {printf("%s: ERROR\n", yytext);} %% /*** end ***/ int yywrap() { return 1; } int main(int argc, char **argv) { if (argc > 1) { if (!(yyin = fopen(argv[1], "r"))) { perror(argv[1]); return 1; } } while (yylex()); return 0; }
在上面的例子中,如果识别到一个字符串while,从正规式的定义可以发现,这个字符串可以与两个正规式匹配,分别是代表标识符的CHARCON和代表while关键字的WHILESYM。此时flex分析器会根据这两个匹配结果再规则中逐一查找,首先找到的是WHILESYM,因此这个字符串被解释为关键字while而不是标识符while。
1 2 3 4 5 6 7 8 %{ Prologue 定义段 %} Bison declarations Bison声明区 %% Grammar rules 规则段 %% Epilogue 用户子程序段
示例:(编译原理试验lab-1,task-5)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 %{ #include <ctype.h> #include <stdio.h> #include <math.h> int yylex (void); void yyerror (char const *); %} %token NUM %define api.value.type {double} %left '+' '-' %left '*' '/' %right 'n' %right '^' %% /* Grammar rules and actions follow. */ input: %empty | input line ; line: '\n' | exp '\n' { printf ("%.10g\n", $1); } ; exp: NUM {$$ = $1;} |exp exp '+' {$$=$1+$2;} |exp exp '-' {$$=$1-$2;} |exp exp '*' {$$=$1*$2;} |exp exp '/' {$$=$1/$2;} |exp exp '^' {$$=pow($1, $2);} |exp 'n' {$$=-$1;} ; %% /* The lexical analyzer returns a double floating point number on the stack and the token NUM, or the numeric code of the character read if not a number. It skips all blanks and tabs, and returns 0 for end-of-input. */ int yylex (void) { int c; /* Skip white space. */ while ((c = getchar ()) == ' ' || c == '\t') continue; /* Process numbers. */ if (c == '.' || isdigit (c)) { ungetc (c, stdin); scanf ("%lf", &yylval); return NUM; } /* Return end-of-input. */ if (c == EOF) return 0; if (c == '!') return 0; /* Return a single char. */ return c; } int main (int argc, char** argv) { yyparse(); return 0; } /* Called by yyparse on error. */ void yyerror (char const *s) { fprintf (stderr, "%s\n", s); }
各个段的用途:
定义段:包含C和C++头文件、全局文件、全局变量、类型定义、词法分析器yylex和错误打印函数声明。
声明区:定义之后需要用到的终结符、非终结符和操作符优先级,以%开头表示类型属性:
%token NUM /*定义终结符NUM*/ %nonassoc ‘<’ /*表示该终结符无结合性,不能出现a<b<c*/ %left ‘+’ ‘-’ /*左结合,a+b+c=(a+b)+c*/ %left ‘*’ ‘/’ /*规则4在3下面,操作符比其上的优先级高*/ %right NEG /*NEG表示非*/ %right ‘^’ /*幂运算右结合;最下面,优先级最高*/
语法规则段:定义了文法的规则。如上面的实例所示,一条规则的格式如下:
左式:左式名:
右式:候选式1 {语义} | 候选式2 {语义} | ...;
其中语义内$$表示这条规则对应的语义输出结果,$n(n为正整数)表示这条规则右式第几个符号的值。如上例中有一条规则是exp:exp exp + {$$=$1+$2}表示这条规则表示的语义是第一个符号和第二个符号(均为exp)的和。
用户代码段:定义前面定义段中声明的函数,或者也可以定义其他代码。
下面是更加全面的例子:(编译原理实验lab-1,task-7)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 %{ /* Filename:lab107.y Author: Date: Makefile: ______________ scanner:lab107.l lab107.y bison -v -d lab107.y flex lab107.l gcc -o scanner 406.tab.c lex.yy.c -lm -lfl .PHONY:clean clean: rm scanner lab107.tab.c lex.yy.c lab107.tab.h _______________ Description: */ // Notice: '-' using as -5+2=-3 ;or 5-2, need something special. By LM. 2021 using // with %precedence NEG used as the highest token, higher than '^', then we can get -2^2=4; without %prec NEG in the rule, SUB is lower than ^, then -2^2=-4 #include <stdio.h> #include <math.h> extern int yylineno; int yylex(); void yyerror(const char *s); %} %define api.value.type {double} %token NUM %token EOL %token ADD %token SUB %token MUL %token DIV %token EXPO %token LP %token RP %% calclist: %empty |calclist exp EOL {printf("=%.10g\n",$2);} exp:term {$$=$1;} |exp ADD term {$$=$1+$3;} |exp SUB term {$$=$1-$3;} |error {} ; term:term2 {$$=$1;} |term MUL term2 {$$=$1*$3;} |term DIV term2 {$$=$1/$3;} ; term2: term3 {$$=$1;} |term3 EXPO term2 {$$=pow($1, $3);} term3: NUM {$$=$1;} |SUB term3 {$$=-1*$2;} %% int main(int args,char **argv){ yyparse(); return 0; } void yyerror(char const *s){ fprintf(stderr,"MyError:%s yylineno:%d\n",s,yylineno); }
注意上面例子中yyerror函数内的yylineno指当前所在行数。
例-1:(课本课后习题3-5)给出下列文法对应的正规式:S → a A S\rightarrow aA S → a A A → b A ∣ a B ∣ b A\rightarrow bA|aB|b A → b A ∣ a B ∣ b B → a A B\rightarrow aA B → a A
解:B B B A → b A ∣ a a A ∣ b A\rightarrow bA|aaA|b A → b A ∣ a a A ∣ b A → ( b ∣ a a ) A ∣ b A\rightarrow (b|aa)A|b A → ( b ∣ a a ) A ∣ b A = ( b ∣ a a ) ∗ b A=(b|aa)^*b A = ( b ∣ a a ) ∗ b S = a ( b ∣ a a ) ∗ b S=a(b|aa)^*b S = a ( b ∣ a a ) ∗ b
例-2:将例-1中求出的正规式转化为正规文法。a ( b ∣ a a ) ∗ a(b|aa)^* a ( b ∣ a a ) ∗ ( b ∣ a a ) ∗ b (b|aa)^*b ( b ∣ a a ) ∗ b
如果处理a ( b ∣ a a ) ∗ a(b|aa)^* a ( b ∣ a a ) ∗ S → A b S\rightarrow Ab S → A b A → a ( b ∣ a a ) ∗ A\rightarrow a(b|aa)^* A → a ( b ∣ a a ) ∗ A → A b ∣ A a a ∣ a A\rightarrow Ab|Aaa|a A → A b ∣ A a a ∣ a S → A b S\rightarrow Ab S → A b A → A b ∣ A a a ∣ a A\rightarrow Ab|Aaa|a A → A b ∣ A a a ∣ a
一个正规式可以用多个等价的正规文法进行表示,正规文法之间只有是否简约的区别,表达的含义相同。
如果处理( b ∣ a a ) ∗ b (b|aa)^*b ( b ∣ a a ) ∗ b S → a A S\rightarrow aA S → a A A → b A ∣ a a A ∣ b A\rightarrow bA|aaA|b A → b A ∣ a a A ∣ b
技巧:左/右线性正规文法对a b ∗ ab^* a b ∗ a ∗ b a^*b a ∗ b 对于左线性正规文法而言
处理a b ∗ ab^* a b ∗ A → A b ∣ a A\rightarrow Ab|a A → A b ∣ a
处理a ∗ b a^*b a ∗ b A → B b , B → B a ∣ ε A\rightarrow Bb,B\rightarrow Ba|\varepsilon A → B b , B → B a ∣ ε
对于右线性正规文法而言
处理a b ∗ ab^* a b ∗ A → a B , B → b B ∣ ε A\rightarrow aB,B\rightarrow bB|\varepsilon A → a B , B → b B ∣ ε
处理a ∗ b a^*b a ∗ b A → a A ∣ b A\rightarrow aA|b A → a A ∣ b
由此可见,要想让最终获得的文法的规则数量尽可能少,对于左线性正规文法要避免产生a ∗ b a^*b a ∗ b a b ∗ ab^* a b ∗
由于NFA形式自由,所以正规式与NFA的相互转化比较易于理解和操作,将正规式转化为NFA只需要无脑怼箭头加状态即可,将NFA转化为正规式只需要无脑删状态组表达式即可。只此3条规则就是记不住也可以很容易推导出来。
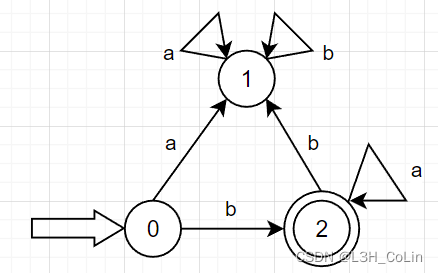
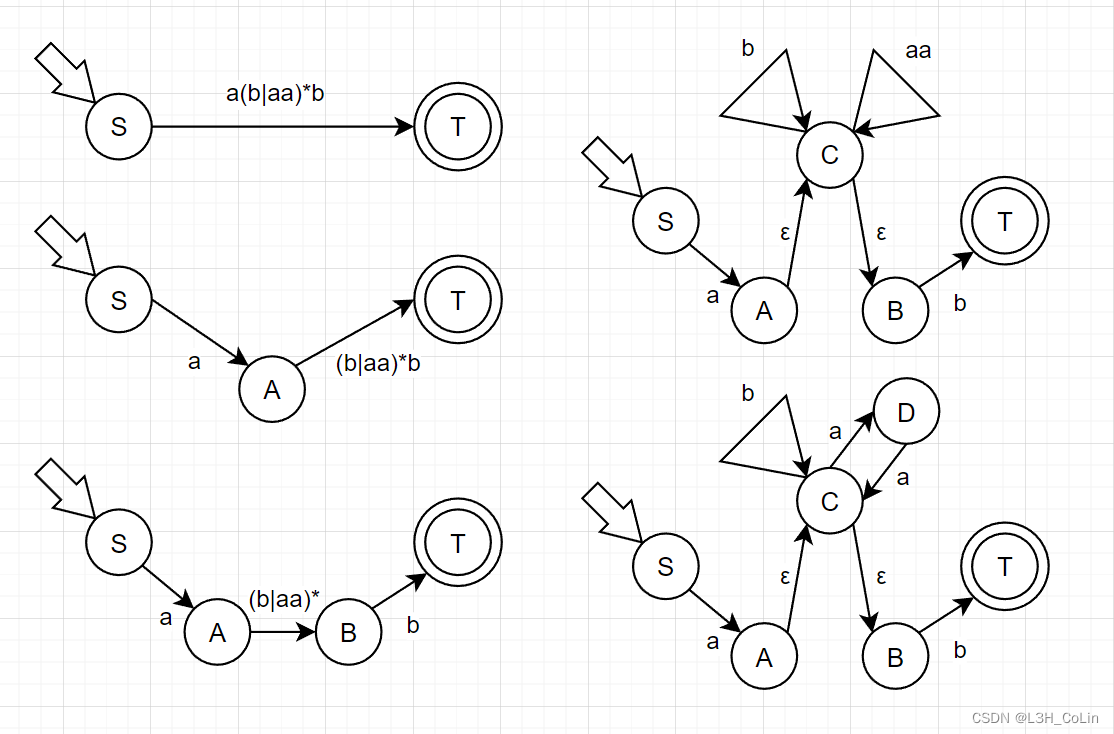
例-3:将例-1中求出的正规式转化为NFA。S S S T T T
例-4:将例-3中求得的NFA还原回正规式。
这部分涉及对ε \varepsilon ε
例-5:将例-3中求得的NFA转化为DFA。
画表构造DFA的状态:
DFA状态名
对应NFA状态集
输入a转到状态集闭包
输入b转到状态集闭包
S S S { S } \{S\} { S } { A , B , C } \{A,B,C\} { A , B , C } 不存在
A A A { A , B , C } \{A,B,C\} { A , B , C } { D } \{D\} { D } { B , C } \{B,C\} { B , C }
B B B { D } \{D\} { D } { B , C } \{B,C\} { B , C } 不存在
C C C { B , C } \{B,C\} { B , C } { D } \{D\} { D } { B , C , T } \{B,C,T\} { B , C , T }
D D D { B , C , T } \{B,C,T\} { B , C , T } { D } \{D\} { D } { B , C , T } \{B,C,T\} { B , C , T }
注意这里画表的流程:画完一行之后如果发现后面两行生成的状态集闭包还有没有被DFA收为状态集的,在DFA中定义新的状态,对应NFA状态集就是这个状态集。在第一行画完后发现输入a转到状态集闭包{ A , B , C } \{A,B,C\} { A , B , C } { A , B , C } \{A,B,C\} { A , B , C } { D } \{D\} { D } { B , C } \{B,C\} { B , C }
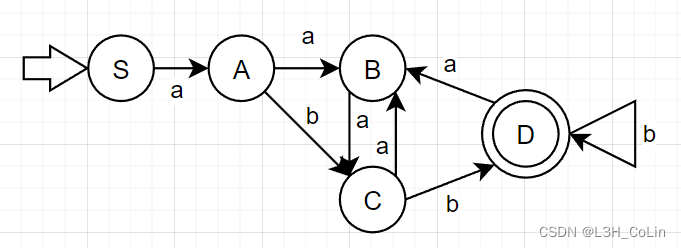
接下来画出该NFA等价的DFA:
DFA化简实际上就是一个不断划分子集的过程。
例-6:将例-5中求得的DFA化简为最简DFA。
分析:化简DFA的第一步就是将终态和非终态划分为两个集合,在上图中就应该是{ S , A , B , C } \{S,A,B,C\} { S , A , B , C } { D } \{D\} { D } { D } \{D\} { D }
首先看非终态集4个状态接受符号a a a S → a A S\stackrel{a}\rightarrow A S → a A A → a B A\stackrel{a}\rightarrow B A → a B B → a C B\stackrel{a}\rightarrow C B → a C C → a B C\stackrel{a}\rightarrow B C → a B { A , B , C } ⊂ { S , A , B , C } \{A,B,C\}\subset\{S,A,B,C\} { A , B , C } ⊂ { S , A , B , C } { S , A , B , C } a = { A , B , C } \{S,A,B,C\}a=\{A,B,C\} { S , A , B , C } a = { A , B , C } b b b A → b C A\stackrel{b}\rightarrow C A → b C C → a D C\stackrel{a}\rightarrow D C → a D { S , A , B , C } b = { C , D } \{S,A,B,C\}b=\{C,D\} { S , A , B , C } b = { C , D } D D D { S , A , B , C } \{S,A,B,C\} { S , A , B , C } b b b A A A C C C A A A C C C a a a S → a A S\stackrel{a}\rightarrow A S → a A B → a C B\stackrel{a}\rightarrow C B → a C S S S B B B 有时在DFA中,某些状态可能不能接受一些符号的输入,如本题中状态B B B b b b { B , C } a = { B , C } \{B,C\}a=\{B,C\} { B , C } a = { B , C } B B B C C C A A A a a a b b b 在本题中,已经确定A A A C C C S S S B B B S S S B B B b b b S S S B B B A A A C C C
注意状态等价的定义: 一个集合中任意两个状态等价当且仅当对于任意输入,任意两个状态到达的下一个状态都相等。一个不接受某个符号输入的状态和一个接受该符号输入的状态一定不在一个状态集中!
前面已经通过例题介绍了正规文法到正规式、正规式到有穷自动机的转换,如果不嫌麻烦可以用两次转换实现本问题。但更好的方法是直接进行转换。
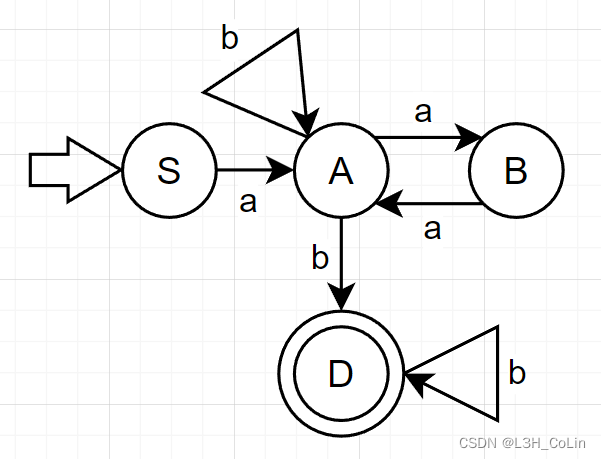
例-7:将例-1中的正规文法转换为NFA。S → a A S\rightarrow aA S → a A A → b A ∣ a B ∣ b A\rightarrow bA|aB|b A → b A ∣ a B ∣ b B → a A B\rightarrow aA B → a A 第一步需要明确开始符号S S S S → a A S\rightarrow aA S → a A S S S a a a A A A S → a A S\stackrel{a}\rightarrow A S → a A S → A a S\rightarrow Aa S → A a S S S a a a A → a S A\stackrel{a}\rightarrow S A → a S 由此可以推断出本题的S S S A A A B B B T T T
凡是A → a B A\rightarrow aB A → a B A → a B A\stackrel{a}\rightarrow B A → a B A → B a A\rightarrow Ba A → B a B → a A B\stackrel{a}\rightarrow A B → a A 可以画出下面的NFA:
与例-3中画出的NFA等价。
例-8:将例-7中求出的NFA转换为正规文法。
由S → a A S\stackrel{a}\rightarrow A S → a A S → a A S\rightarrow aA S → a A A → a B A\stackrel{a}\rightarrow B A → a B A → a B A\rightarrow aB A → a B A → b A A\stackrel{b}\rightarrow A A → b A A → b A A\rightarrow bA A → b A B → a A B\stackrel{a}\rightarrow A B → a A B → a A B\rightarrow aA B → a A A → b T A\stackrel{b}\rightarrow T A → b T A → b A\rightarrow b A → b
求得正规文法:S → a A S\rightarrow aA S → a A A → b A ∣ a B ∣ b A\rightarrow bA|aB|b A → b A ∣ a B ∣ b B → a A B\rightarrow aA B → a A
在考试中,很可能会结合实验的内容进行设计,如标识符识别、关键字识别等实用的例子。
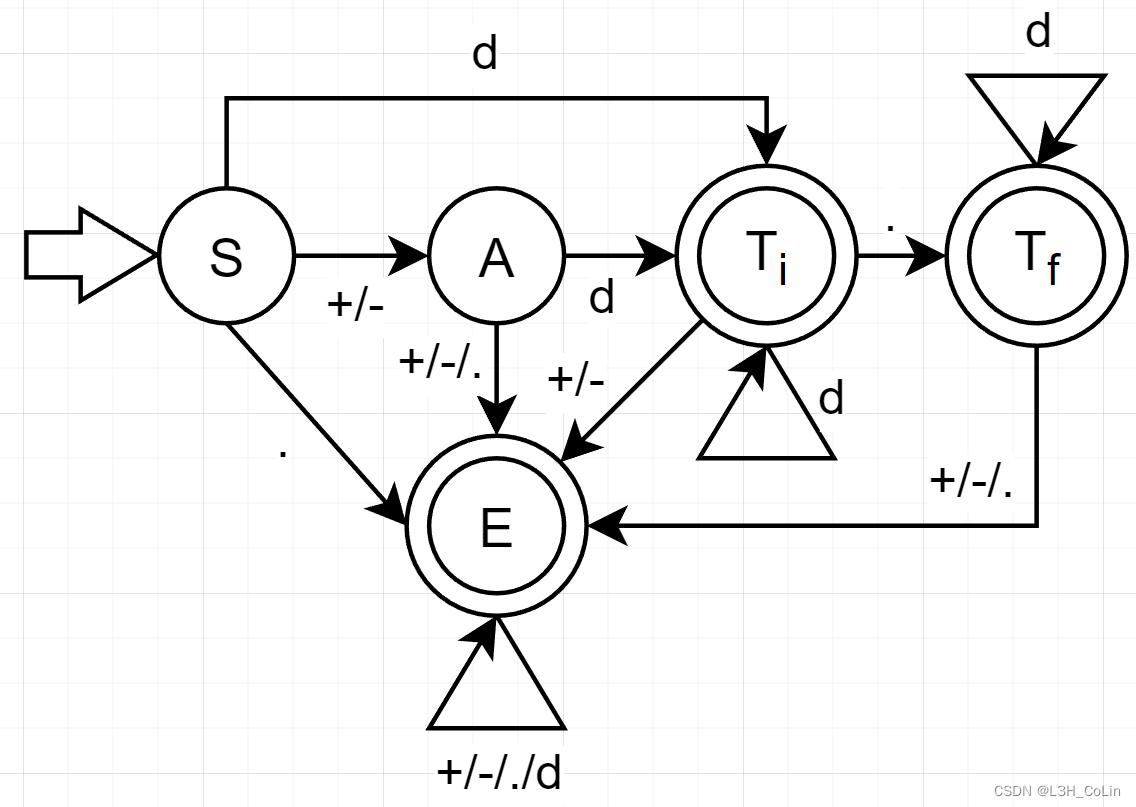
例-9(综合例题):在编译原理实验1中,我们完成了对一门小语言的词法分析程序,有关其中对于数字(含正负数、浮点数)的识别,回答下列问题:(1) 设初态为S S S T i , T f T_i,T_f T i , T f E E E d d d { d , . , + , − } \{d,.,+,-\} { d , . , + , − }
解:要做本题,首先要搞清楚字符出现的顺序与规律。这里面正负号或者不出现,或者出现在第一位,小数点最多只会出现1次,且只要出现小数点,就必然要识别为浮点数,否则识别为整数。
整数的格式:正负号(可选)+若干位数字
注意到两种识别前面有相同的一部分,所以可以合并前面的识别部分。
将识别正负号作为一个状态,识别整数部分作为一个状态,识别小数点作为一个状态,识别小数部分作为一个状态,画出如下NFA:
注意这里的画图技巧:当识别到一个状态发现前面的句子已经能够识别出来,就将这个状态设置为终态。 这样可以减少一些状态的设置。另外,最好让任何一个状态接收任何一个输入都有意义, 如这里的终态E E E
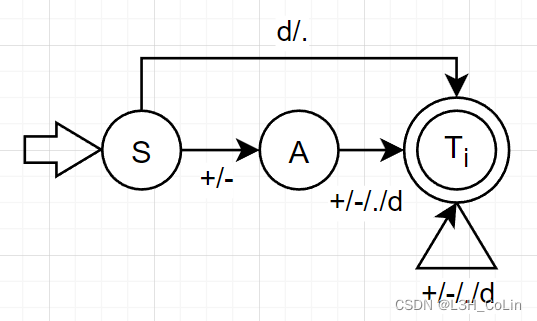
(2) 你第1题画出来的NFA是否是DFA?若是,说明理由并化简DFA,若不是,将其转换为DFA并化简。画出最简DFA。化简之后想一想使用最简DFA去识别数字是否合适?为什么?
分析:图中并没有一个状态对于一个输入有多个输出的情况,因此这是一个DFA。下面来判断一下这个DFA是否可以化简。
首先划分终态集{ E , T i , T f } \{E,T_i,T_f\} { E , T i , T f } { S , A } \{S,A\} { S , A } S S S A A A A A A { { S } , { A } , { E , T i , T f } } \{\{S\},\{A\},\{E,T_i,T_f\}\} { { S } , { A } , { E , T i , T f } }
这个最简DFA识别数字并不实用,因为它将所有数字以及错误情况全部识别为一个终态,这样无法将整数、浮点数与错误这三种情况区分开,因此在实际应用中还是应该使用第1题中求出的DFA。
(3) 根据前面两题的结果,补全下面的bison代码,用于识别上面的数字。(方括号内为答案,后接题目序号)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 %{ #include <stdio.h> #include <math.h> extern int yylineno; int yylex(); void yyerror(const char *s); %} %token num // 0-9这10个数字字符 %token plus // 加号 %token minus // 减号 %token dot // 小数点 %% unsigned_integer: num {$$ = $2.value;} // .value属性为字符对应的数值 | unsigned_integer num {[$$ = $1 * 10 + $2;]<1>} number: [plus number]<2> {$$=$2;} | [minus number]<3> {$$=-$2;} | unsigned_integer dot unsigned_integer {$$=$1 + $3 * 1.0 / pow(10, $3.length);} // $2.length表示[小数位的总位数]<4> %% ......