出现于2017、2019、2020、2021年第一题,重点在于重合指数的计算。
在确定的文本中,重合指数的定义如下:
重合指数 :文本中任选两个字符相同的概率。通过概率论相关知识容易得到其公式为
I c ( X ) = ∑ i = 0 25 f i ( f i − 1 ) n ( n − 1 ) I_c(X)=\frac{\sum_{i=0}^{25}f_i(f_i-1)}{n(n-1)}
I c ( X ) = n ( n − 1 ) ∑ i = 0 2 5 f i ( f i − 1 )
其中f i f_i f i n n n
求逆置换和解密不难,解密根据逆置换分组重排即可。
出现于2018年第一题,重点在于通过加密密钥求出解密密钥。
如果加密密钥为( a , b ) (a, b) ( a , b ) p p p c c c
c = a p + b ( m o d 26 ) c = ap+b\pmod {26}
c = a p + b ( m o d 2 6 )
经过推导容易得出:
p = a − 1 ( c − b ) ( m o d 26 ) p = a^{-1}(c-b)\pmod {26}
p = a − 1 ( c − b ) ( m o d 2 6 )
解密密钥为( a − 1 , − a − 1 b ) (a^{-1}, -a^{-1}b) ( a − 1 , − a − 1 b )
另外注意A对应的数为0不是1。
出现于2017、2019、2020、2021年第二题,重点在于LSFR生成规则的获取。(今年周期不考)
首先将明文与密文异或得到密钥,题目中会给出LFSR的级数,这也是后面计算的矩阵的行数和列数。为描述方便,以2021年第二题为例讲解。
题中的密钥为001110011011111,级数为5,故以5位单位分组,可以分为3组。设递推公式为
a 5 = c 5 a 0 ⊕ c 4 a 1 ⊕ . . . ⊕ c 1 a n − 1 , c i ∈ Z 2 , c 5 = 1 a_{5}=c_5a_0\oplus c_4a_1\oplus ...\oplus c_1a_{n-1},c_i\in Z_2,c_5=1
a 5 = c 5 a 0 ⊕ c 4 a 1 ⊕ . . . ⊕ c 1 a n − 1 , c i ∈ Z 2 , c 5 = 1
将其转换为矩阵形式:
a 5 = ( c 5 c 4 c 3 c 2 c 1 ) ( a 0 a 1 a 2 a 3 a 4 ) a_5=\begin{pmatrix}c_5 & c_4 & c_3 & c_2 & c_1\end{pmatrix}
\begin{pmatrix}a_0\\
a_1\\
a_2\\
a_3\\
a_4\end{pmatrix} a 5 = ( c 5 c 4 c 3 c 2 c 1 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ a 0 a 1 a 2 a 3 a 4 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
扩展到第二组全部5位可以得到:
( a 5 a 6 a 7 a 8 a 9 ) = ( c 5 c 4 c 3 c 2 c 1 ) ( a 0 a 1 a 2 a 3 a 4 a 1 a 2 a 3 a 4 a 5 a 2 a 3 a 4 a 5 a 6 a 3 a 4 a 5 a 6 a 7 a 4 a 5 a 6 a 7 a 8 ) \begin{pmatrix}a_5 & a_6 & a_7 & a_8 & a_9\end{pmatrix}
=\begin{pmatrix}c_5 & c_4 & c_3 & c_2 & c_1\end{pmatrix}
\begin{pmatrix}a_0&a_1&a_2&a_3&a_4\\
a_1&a_2&a_3&a_4&a_5\\
a_2&a_3&a_4&a_5&a_6\\
a_3&a_4&a_5&a_6&a_7\\
a_4&a_5&a_6&a_7&a_8\end{pmatrix} ( a 5 a 6 a 7 a 8 a 9 ) = ( c 5 c 4 c 3 c 2 c 1 ) ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ a 0 a 1 a 2 a 3 a 4 a 1 a 2 a 3 a 4 a 5 a 2 a 3 a 4 a 5 a 6 a 3 a 4 a 5 a 6 a 7 a 4 a 5 a 6 a 7 a 8 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
以此来计算c i c_i c i Z 2 Z_2 Z 2 行列变换法 较伴随矩阵法更方便,且不易出错。
特征多项式:f ( x ) = ∣ x I − T ∣ = x n − c 1 x n − 1 − . . . − c n − 1 x − c n f(x)=|xI-T|=x^n-c_1x^{n-1}-...-c_{n-1}x-c_n f ( x ) = ∣ x I − T ∣ = x n − c 1 x n − 1 − . . . − c n − 1 x − c n
出现于2018年第二题,重点在于通过加密密钥求出解密密钥。
需要注意的是,如果密钥矩阵的长度为m,则需要m组明文-密文对,把它们组成一个方阵,计算逆矩阵即可求解。如果方阵奇异,则需要重新选择明文-密文对组成方阵。
技巧 :求26的模逆矩阵,对2阶和3阶方阵使用伴随矩阵法 更方便。考虑到计算量,考试应该不会考高于3阶方阵的模26逆矩阵。
出现于2017、2018、2019、2020年第三题。要牢记熵、信息量、互信息的概念和有关公式,当公式记不清楚的时候通过概念可能可以推出来。这一部分难点在于对公式的灵活运用。
定义 :一个密码体制具有完全保密性,如果对于任意x ∈ P x\in P x ∈ P y ∈ C y \in C y ∈ C P r [ x ∣ y ] = P r [ x ] Pr[x|y]=Pr[x] P r [ x ∣ y ] = P r [ x ]
定理1:假设移位密码的26个密钥以相同概率随机使用,对于任意的明文概率分布,移位密码都具有完善保密性。
定理2:假设密码体制( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) ∣ K ∣ = ∣ C ∣ = ∣ P ∣ |K|=|C|=|P| ∣ K ∣ = ∣ C ∣ = ∣ P ∣ ∣ K ∣ ≥ ∣ C ∣ ≥ ∣ P ∣ |K|\ge |C|\ge |P| ∣ K ∣ ≥ ∣ C ∣ ≥ ∣ P ∣ 1 ∣ K ∣ \frac{1}{|K|} ∣ K ∣ 1 x ∈ P , y ∈ C x\in P,y\in C x ∈ P , y ∈ C k k k e k ( x ) = y e_k(x)=y e k ( x ) = y
判定定理1:对密码体制( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) x ∈ P , y ∈ C x\in P,y\in C x ∈ P , y ∈ C ∑ k : x = d k ( y ) P r [ k ] = 1 ∣ P ∣ \sum_{k:x=d_k(y)}Pr[k]=\frac{1}{|P|} ∑ k : x = d k ( y ) P r [ k ] = ∣ P ∣ 1
判定定理2:对于密码体制( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) K K K x ∈ P , y ∈ C , ∣ k : x = d k ( y ) ∣ = ∣ K ∣ ∣ P ∣ x\in P,y\in C,|{k:x=d_k(y)}|=\frac{|K|}{|P|} x ∈ P , y ∈ C , ∣ k : x = d k ( y ) ∣ = ∣ P ∣ ∣ K ∣ (可以由判定定理1推导出)
判定定理3:对于密码体制( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) ∣ P ∣ = ∣ C ∣ |P|=|C| ∣ P ∣ = ∣ C ∣ K K K 当且仅当 对于任意的x ∈ P , y ∈ C , ∣ k : x = d k ( y ) ∣ = ∣ K ∣ ∣ P ∣ x\in P,y\in C,|{k:x=d_k(y)}|=\frac{|K|}{|P|} x ∈ P , y ∈ C , ∣ k : x = d k ( y ) ∣ = ∣ P ∣ ∣ K ∣ (可以由判定定理4推导出)
判定定理4:对于密码体制( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) ∣ P ∣ = ∣ C ∣ |P|=|C| ∣ P ∣ = ∣ C ∣ ∣ P ∣ |P| ∣ P ∣ 当且仅当 对于任意x ∈ P , y ∈ C x\in P,y\in C x ∈ P , y ∈ C ∑ k : x = d k ( y ) P r [ k ] = 1 ∣ P ∣ \sum_{k:x=d_k(y)}Pr[k]=\frac{1}{|P|} ∑ k : x = d k ( y ) P r [ k ] = ∣ P ∣ 1
如果信源发出消息x i x_i x i p ( x i ) p(x_i) p ( x i )
I ( x i ) = log 2 1 p ( x i ) = − log 2 p ( x i ) I(x_i)=\log_2\frac{1}{p(x_i)}=-\log_2p(x_i)
I ( x i ) = log 2 p ( x i ) 1 = − log 2 p ( x i )
(式中的底数可以换,这里由于使用比特作为信息媒介,因此使用2作为底数。如果使用10进制数字,则就应使用10作为底数,即底数由1位信息媒介的可能取值数决定)
联合自信息量 :
I ( x 1 x 2 . . . x n ) = − log 2 p ( x 1 x 2 . . . x n ) I(x_1x_2...x_n)=-\log_2p(x_1x_2...x_n)
I ( x 1 x 2 . . . x n ) = − log 2 p ( x 1 x 2 . . . x n )
当这些变量均独立时,I ( x 1 x 2 . . . x n ) = I ( x 1 ) + I ( x 2 ) + . . . + I ( x n ) I(x_1x_2...x_n)=I(x_1)+I(x_2)+...+I(x_n) I ( x 1 x 2 . . . x n ) = I ( x 1 ) + I ( x 2 ) + . . . + I ( x n )
条件自信息量: I ( x i ∣ y j ) = − log 2 p ( x i ∣ y j ) I(x_i|y_j)=-\log_2p(x_i|y_j) I ( x i ∣ y j ) = − log 2 p ( x i ∣ y j ) I ( y j ∣ x i ) = − log 2 p ( y j ∣ x i ) I(y_j|x_i)=-\log_2p(y_j|x_i) I ( y j ∣ x i ) = − log 2 p ( y j ∣ x i ) I ( x i y j ) = − log 2 p ( y j ∣ x i ) p ( x i ) = I ( x i ) + I ( y j ∣ x i ) = I ( y j ) + I ( x i ∣ y j ) I(x_iy_j)=-\log_2p(y_j|x_i)p(x_i)=I(x_i)+I(y_j|x_i)=I(y_j)+I(x_i|y_j) I ( x i y j ) = − log 2 p ( y j ∣ x i ) p ( x i ) = I ( x i ) + I ( y j ∣ x i ) = I ( y j ) + I ( x i ∣ y j )
互信息量:
I ( x i ; y j ) = I ( x i ) − I ( x i ∣ y j ) = log 2 p ( x i ∣ y j ) p ( x i ) = log 2 p ( x i y j ) p ( x i ) p ( y j ) I(x_i;y_j)=I(x_i)-I(x_i|y_j)=\log_2\frac{p(x_i|y_j)}{p(x_i)}=\log_2\frac{p(x_iy_j)}{p(x_i)p(y_j)}
I ( x i ; y j ) = I ( x i ) − I ( x i ∣ y j ) = log 2 p ( x i ) p ( x i ∣ y j ) = log 2 p ( x i ) p ( y j ) p ( x i y j )
即先验不确定度− - −
即信息量的期望。
H ( X ) = E [ I ( x ) ] = − ∑ x ∈ X p ( x ) ( log 2 p ( x ) ) H(X)=E[I(x)]=-\sum_{x\in X}p(x)(\log_2p(x))
H ( X ) = E [ I ( x ) ] = − x ∈ X ∑ p ( x ) ( log 2 p ( x ) )
条件熵 :
H ( X ∣ Y ) = − ∑ x ∈ X ∑ y ∈ Y p ( x y ) log 2 p ( x ∣ y ) H(X|Y)=-\sum_{x\in X}\sum_{y\in Y}p(xy)\log_2p(x|y)
H ( X ∣ Y ) = − x ∈ X ∑ y ∈ Y ∑ p ( x y ) log 2 p ( x ∣ y )
注意上面的式子是条件熵,下面的不是!
H ( X ∣ y ) = − ∑ x ∈ X p ( x ∣ y ) log 2 p ( x ∣ y ) H(X|y)=-\sum_{x\in X}p(x|y)\log_2p(x|y)
H ( X ∣ y ) = − x ∈ X ∑ p ( x ∣ y ) log 2 p ( x ∣ y )
定理1 :随机变量X X X p 1 , p 2 , . . . , p n p_1,p_2,...,p_n p 1 , p 2 , . . . , p n H ( X ) ≤ log 2 n H(X)\le \log_2n H ( X ) ≤ log 2 n p i = 1 n p_i=\frac{1}{n} p i = n 1
定理2 :H ( X Y ) ≤ H ( X ) + H ( Y ) H(XY)\le H(X)+H(Y) H ( X Y ) ≤ H ( X ) + H ( Y ) X X X Y Y Y
定理3 :H ( X Y ) = H ( Y ) + H ( X ∣ Y ) H(XY)=H(Y)+H(X|Y) H ( X Y ) = H ( Y ) + H ( X ∣ Y )
定理4 :H ( X ∣ Y ) ≤ H ( X ) H(X|Y)\le H(X) H ( X ∣ Y ) ≤ H ( X ) X X X Y Y Y
即互信息量的期望
I ( X ; Y ) = E [ I ( x ; y ) ] = ∑ x ∈ X ∑ y ∈ Y p ( x y ) I ( x ; y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X Y ) I(X;Y)=E[I(x;y)]=\sum_{x\in X}\sum_{y\in Y}p(xy)I(x;y)\\
=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(XY) I ( X ; Y ) = E [ I ( x ; y ) ] = x ∈ X ∑ y ∈ Y ∑ p ( x y ) I ( x ; y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X Y )
性质:I ( X ; Y ) = I ( Y ; X ) ≤ min { H ( X ) , H ( Y ) } I(X;Y)=I(Y;X)\le \min\{H(X),H(Y)\} I ( X ; Y ) = I ( Y ; X ) ≤ min { H ( X ) , H ( Y ) } I ( X ; Y ) = H ( X ) = H ( Y ) I(X;Y)=H(X)=H(Y) I ( X ; Y ) = H ( X ) = H ( Y )
平均条件互信息量:I ( X ; Y ∣ Z ) = I ( X ; Y Z ) − I ( X ; Z ) I(X;Y|Z)=I(X;YZ)-I(X;Z) I ( X ; Y ∣ Z ) = I ( X ; Y Z ) − I ( X ; Z )
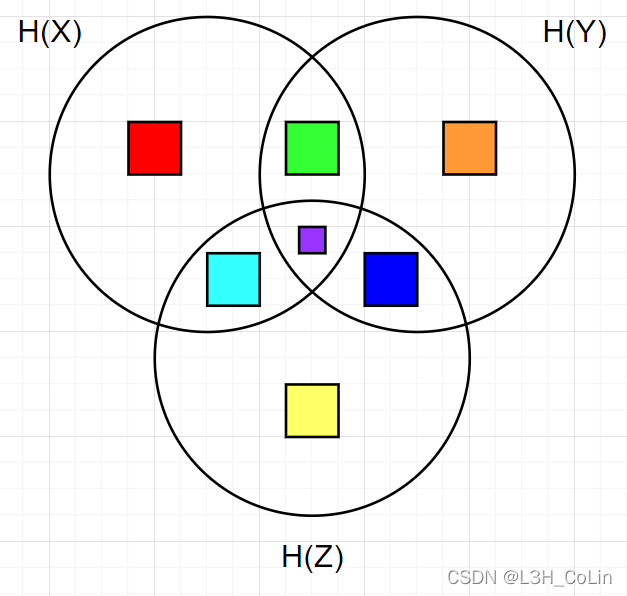
I ( X ; Y ) I(X;Y) I ( X ; Y ) I ( Y ; Z ) I(Y;Z) I ( Y ; Z ) I ( X ; Z ) I(X;Z) I ( X ; Z ) I ( X ; Y ∣ Z ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( z ) p ( x y z ) p ( x z ) p ( y z ) I(X;Y|Z)=\sum_{x\in X}\sum_{y\in Y}\sum_{z\in Z}p(xyz)\log_2\frac{p(z)p(xyz)}{p(xz)p(yz)} I ( X ; Y ∣ Z ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( x z ) p ( y z ) p ( z ) p ( x y z ) I ( Y ; Z ∣ X ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( x ) p ( x y z ) p ( x y ) p ( x z ) I(Y;Z|X)=\sum_{x\in X}\sum_{y\in Y}\sum_{z\in Z}p(xyz)\log_2\frac{p(x)p(xyz)}{p(xy)p(xz)} I ( Y ; Z ∣ X ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( x y ) p ( x z ) p ( x ) p ( x y z ) I ( X ; Z ∣ Y ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( y ) p ( x y z ) p ( y x ) p ( y z ) I(X;Z|Y)=\sum_{x\in X}\sum_{y\in Y}\sum_{z\in Z}p(xyz)\log_2\frac{p(y)p(xyz)}{p(yx)p(yz)} I ( X ; Z ∣ Y ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( y x ) p ( y z ) p ( y ) p ( x y z ) H ( X ∣ Y Z ) H(X|YZ) H ( X ∣ Y Z ) H ( Y ∣ X Z ) H(Y|XZ) H ( Y ∣ X Z ) H ( Z ∣ X Y ) H(Z|XY) H ( Z ∣ X Y ) I ( X ; Y ; Z ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( x y ) p ( y z ) p ( z x ) p ( x ) p ( y ) p ( z ) p ( x y z ) I(X;Y;Z)=\sum_{x\in X}\sum_{y\in Y}\sum_{z\in Z}p(xyz)\log_2\frac{p(xy)p(yz)p(zx)}{p(x)p(y)p(z)p(xyz)} I ( X ; Y ; Z ) = ∑ x ∈ X ∑ y ∈ Y ∑ z ∈ Z p ( x y z ) log 2 p ( x ) p ( y ) p ( z ) p ( x y z ) p ( x y ) p ( y z ) p ( z x ) H ( X ∣ Y ) H(X|Y) H ( X ∣ Y ) H ( Y ∣ X ) H(Y|X) H ( Y ∣ X ) H ( X ∣ Z ) H(X|Z) H ( X ∣ Z ) H ( Z ∣ X ) H(Z|X) H ( Z ∣ X ) H ( Y ∣ Z ) H(Y|Z) H ( Y ∣ Z ) H ( Z ∣ Y ) H(Z|Y) H ( Z ∣ Y ) H ( X Y ) H(XY) H ( X Y ) H ( Y Z ) H(YZ) H ( Y Z ) H ( X Z ) H(XZ) H ( X Z ) I ( X Y ; Z ) I(XY;Z) I ( X Y ; Z ) I ( X Z ; Y ) I(XZ;Y) I ( X Z ; Y ) I ( Y Z ; X ) I(YZ;X) I ( Y Z ; X ) H ( X Y ∣ Z ) H(XY|Z) H ( X Y ∣ Z ) H ( X Z ∣ Y ) H(XZ|Y) H ( X Z ∣ Y ) H ( Y Z ∣ X ) H(YZ|X) H ( Y Z ∣ X )
由上图可知以下结论:I ( X ; Y ; Z ) = I ( X ; Z ) − I ( X ; Z ∣ Y ) = I ( X ; Y ) − I ( X ; Y ∣ Z ) = I ( Y ; Z ) − I ( Y ; Z ∣ X ) I(X;Y;Z)=I(X;Z)-I(X;Z|Y)=I(X;Y)-I(X;Y|Z)=I(Y;Z)-I(Y;Z|X) I ( X ; Y ; Z ) = I ( X ; Z ) − I ( X ; Z ∣ Y ) = I ( X ; Y ) − I ( X ; Y ∣ Z ) = I ( Y ; Z ) − I ( Y ; Z ∣ X ) H ( X ∣ Y ) − H ( X ∣ Y Z ) = I ( X ; Z ∣ Y ) H(X|Y)-H(X|YZ)=I(X;Z|Y) H ( X ∣ Y ) − H ( X ∣ Y Z ) = I ( X ; Z ∣ Y ) H ( Y ∣ Z ) − H ( Y ∣ Z X ) = I ( Y ; X ∣ Z ) H(Y|Z)-H(Y|ZX)=I(Y;X|Z) H ( Y ∣ Z ) − H ( Y ∣ Z X ) = I ( Y ; X ∣ Z ) H ( Z ∣ X ) − H ( Z ∣ X Y ) = I ( Z ; Y ∣ X ) H(Z|X)-H(Z|XY)=I(Z;Y|X) H ( Z ∣ X ) − H ( Z ∣ X Y ) = I ( Z ; Y ∣ X ) I ( X ; Y ) + I ( Z ; Y ∣ X ) = I ( X Z ; Y ) I(X;Y)+I(Z;Y|X)=I(XZ;Y) I ( X ; Y ) + I ( Z ; Y ∣ X ) = I ( X Z ; Y ) I ( Y ; Z ) + I ( X ; Z ∣ Y ) = I ( X Y ; Z ) I(Y;Z)+I(X;Z|Y)=I(XY;Z) I ( Y ; Z ) + I ( X ; Z ∣ Y ) = I ( X Y ; Z ) I ( Z ; X ) + I ( Y ; X ∣ Z ) = I ( X Z ; Y ) I(Z;X)+I(Y;X|Z)=I(XZ;Y) I ( Z ; X ) + I ( Y ; X ∣ Z ) = I ( X Z ; Y )
定理2.10 ( P , C , K , E , D ) (P,C,K,E,D) ( P , C , K , E , D ) H ( K ∣ C ) = H ( K ) + H ( P ) − H ( C ) H(K|C)=H(K)+H(P)-H(C) H ( K ∣ C ) = H ( K ) + H ( P ) − H ( C )
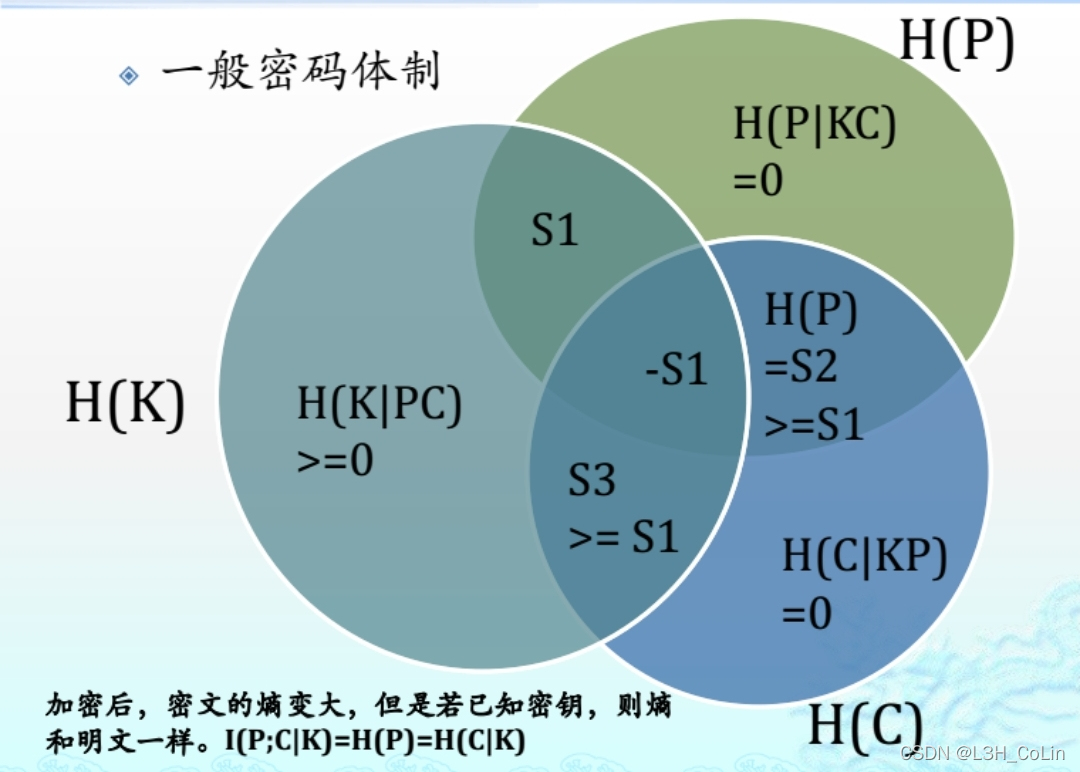
一般密码体制与熵有关的性质
∣ P ∣ ≤ ∣ C ∣ |P|\le|C| ∣ P ∣ ≤ ∣ C ∣ H ( P ∣ K C ) = H ( C ∣ K P ) = 0 H(P|KC)=H(C|KP)=0 H ( P ∣ K C ) = H ( C ∣ K P ) = 0 H ( P K ) = H ( P ) + H ( K ) H(PK)=H(P)+H(K) H ( P K ) = H ( P ) + H ( K ) 定理2.10结论
H ( P ) ≤ H ( C ) ≤ H ( P ) + H ( K ) H(P)\le H(C)\le H(P)+H(K) H ( P ) ≤ H ( C ) ≤ H ( P ) + H ( K ) H ( K ∣ C ) ≤ H ( K ) H(K|C)\le H(K) H ( K ∣ C ) ≤ H ( K ) H ( P ∣ C ) ≤ H ( K ∣ C ) H(P|C)\le H(K|C) H ( P ∣ C ) ≤ H ( K ∣ C )
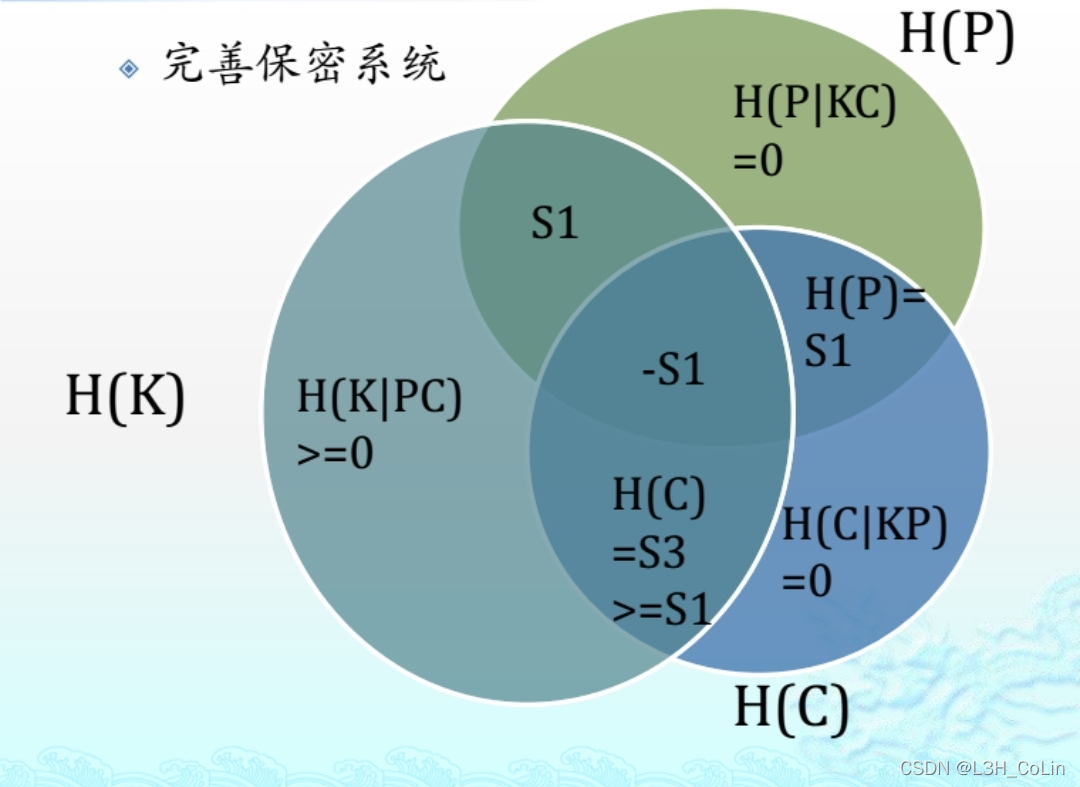
推论:若∣ P ∣ = ∣ C ∣ |P|=|C| ∣ P ∣ = ∣ C ∣ H ( K ∣ C ) = H ( K ) H(K|C)=H(K) H ( K ∣ C ) = H ( K )
H ( P ∣ C ) = H ( P ) H(P|C)=H(P) H ( P ∣ C ) = H ( P ) ∣ P ∣ ≤ ∣ C ∣ ≤ ∣ K ∣ ( P r [ y ∣ x ] = P r [ y ] > 0 ) |P|\le |C|\le |K|(Pr[y|x]=Pr[y]>0) ∣ P ∣ ≤ ∣ C ∣ ≤ ∣ K ∣ ( P r [ y ∣ x ] = P r [ y ] > 0 ) H ( P ) ≤ H ( C ) ≤ H ( K ) H(P)\le H(C)\le H(K) H ( P ) ≤ H ( C ) ≤ H ( K )
注意:密码体制之中有三个随机变量:明文P、密文C和密钥K,三者之间有一定关系:I ( P ; K ) I(P;K) I ( P ; K ) H ( C ∣ P K ) = 0 H(C|PK)=0 H ( C ∣ P K ) = 0 H ( P ∣ C K ) = 0 H(P|CK)=0 H ( P ∣ C K ) = 0 S 3 ≥ S 1 , S 2 ≥ S 1 S3\ge S1,S2\ge S1 S 3 ≥ S 1 , S 2 ≥ S 1 H ( P ∣ C ) = H ( P ) H(P|C)=H(P) H ( P ∣ C ) = H ( P ) I ( P ; C ) = 0 I(P;C)=0 I ( P ; C ) = 0
完善保密性的证明 :使用定义、使用四个判定定理
掌握加密和解密方法。出现于2021年第四题
Rabin加密需要3个参数参与:n,p,q,其中p和q为私钥且均为4k+3型素数,n=pq为公钥。p l a i n t e x t = c i p h e r m o d n plaintext = \sqrt{cipher} \mod n p l a i n t e x t = c i p h e r m o d n c i p h e r m o d p \sqrt{cipher} \mod p c i p h e r m o d p c i p h e r m o d q \sqrt{cipher} \mod q c i p h e r m o d q c i p h e r ≡ c i p h e r p + 1 4 ( m o d p ) , c i p h e r ≡ c i p h e r q + 1 4 ( m o d q ) \sqrt{cipher}\equiv cipher^{\frac{p+1}{4}}\pmod p,\sqrt{cipher}\equiv cipher^{\frac{q+1}{4}}\pmod q c i p h e r ≡ c i p h e r 4 p + 1 ( m o d p ) , c i p h e r ≡ c i p h e r 4 q + 1 ( m o d q )
掌握加密和解密方法,出现于2020年第四题,2017、2018年第五题
通过n解出p和q的值,计算c d m o d n c^d\mod n c d m o d n e d ≡ 1 ( m o d φ ( n ) ) ed\equiv 1\pmod {\varphi(n)} e d ≡ 1 ( m o d φ ( n ) )
出现于2018、2020年第六题,2017年第七题,重点在于逆元的计算。
两题都给了’00’的替换值,通过这个值可以直接获得C的值,然后逐位计算即可。
出现于2017年第七题,2018、2019、2021年第八题,这种题范围广泛,需要我们对各种加密函数、散列函数、密码分析原理等有一定的理解。
需要能说得出基本原理的名词解释,可按照下面列表进行自测:
古典密码加密原理
移位密码
代换密码
仿射密码
维吉尼亚密码
希尔密码
置换密码
古典密码分析原理
移位密码的唯密文攻击原理(暴力破解)
代换密码的唯密文攻击原理(字频分析 )
仿射密码的唯密文攻击原理(字频分析)
维吉尼亚密码的唯密文攻击原理(Kasiski测试法、重合指数法 )
希尔密码的已知明文攻击原理(矩阵计算)
四种密码攻击方式
流密码
LSFR的工作原理
LSFR的变换矩阵、特征多项式分析原理(已知明文攻击)
唯一解距离和乘积密码体制
伪密钥的概念
自然语言的熵和冗余度
自然语言的唯一解距离
乘积密码和幂等密码
线性密码框架
SPN网络的加密过程
Feistel结构的加密过程
线性密码分析
几种线性密码
分组密码的五种工作模式原理与区分
ECB(电子密码本)
CBC(密码分组链接)
CFB(密码反馈)
OFB(输出反馈)
CTR(计数器)
CTS(密文挪用)
Hash函数
Hash函数三个安全性问题
生日攻击原理
MD5基本流程
SHA1基本流程
SHA3基本流程
SM3基本流程
MAC校验码
彩虹表攻击原理与优势
公钥密码体制
中国剩余定理加速解密RSA
Montgomery算法原理
DH密钥交换的实现及中间人攻击原理
素性检测算法
伪素数
Solovay-Strassen算法
Miller-Rabin算法
共模攻击与小加密指数攻击原理
小解密指数的Wiener攻击原理
ElGamal密钥交换原理
数字签名的基本概念与作用
ElGamal数字签名算法原理
DSA数字签名算法原理
PGP基本结构
原理简述:
重点在于计算离散椭圆曲线密码的加和与乘积。
对于椭圆曲线方程y 2 ≡ x 3 + a x + b m o d m y^2\equiv x^3+ax+b\mod m y 2 ≡ x 3 + a x + b m o d m P , Q P,Q P , Q 过两点的直线的斜率:λ = 3 x 2 + a 2 y ( P = Q ) , y Q − y P x Q − x P ( P ≠ Q ) \lambda=\frac{3x^2+a}{2y}(P=Q),\frac{y_Q-y_P}{x_Q-x_P}(P\ne Q) λ = 2 y 3 x 2 + a ( P = Q ) , x Q − x P y Q − y P ( P = Q ) x = λ 2 − x P − x Q x=\lambda^2-x_P-x_Q x = λ 2 − x P − x Q y = λ ( x − x P ) + y P y=\lambda(x-x_P)+y_P y = λ ( x − x P ) + y P
计算加速技巧 :① 写出模域中各个元素的方根,然后进行计算对照即可。如计算y 2 = x 3 + x + 1 m o d 19 y^2=x^3+x+1\mod 19 y 2 = x 3 + x + 1 m o d 1 9 2 k 2^k 2 k