计算机组成原理——第3章

3.1 计算机中的运算

注意移位运算中逻辑移位和算术移位的区别，算术移位不会修改符号位。

3.2 定点加减法运算

3.2.1 补码加减法运算

$$[x]_补+[y]_补=[x+y]_补 \pmod M$$

在以M为模时，两数的补码之和等于两数和的补码。

$$[x-y]_补=[x]_补-[y]_补=[x]_补+[-y]_补 \pmod M$$

3.2.2 溢出及检测

对于补码加法运算（减法可以转化为加法），溢出的检测方式有：

• 当正数与正数相加得到负数，或负数与负数相加得到正数时，有溢出。当两个运算数符号不同时，一定不会发生溢出。
• 根据运算过程中最高数据位的进位和符号位的进位来判断。当最高数据位的进位与符号位的进位不一致时发生溢出。考虑正数加正数的情况，如果结果为负数，说明最高数据位的进位为1，而符号位的进位为0，不一致。若为负数加负数得到正数，则符号位的进位为1，最高数据位的进位为0（否则得到的结果中符号位为1），不一致。
• 使用变形补码，即使用两个二进制数表示数据的符号。正数符号以00表示，负数为11。在运算过程中如果符号位出现了01或10则说明发生了溢出。
• 使用软件的方法判断
• 对于无符号数的溢出，只需要看两者相加后有没有溢出的进位即可。

3.2.3 加减法的逻辑实现

全加器

一位全加器需要接收两个操作数以及上一位的进位，输出该位的结果与下一位的进位。在设计过程中，如果需要使用减法，则将1与第二个操作数异或，然后进行加法操作。

多位串行加法器

将多个全加器串行在一起，上一位的进位传送到下一位的全加器中，多位串行全加器只能一位一位进行加法。

注意如果需要同时实现加法与减法，则增加一个输入标识计算是加法还是减法，0为加法，1为减法。如果需要计算减法，就需要首先计算第二个操作数的相反数的补码。计算一个数相反数的补码的方法是：对这个数所有二进制位取反再加1。因此减法标识位需要加到第一个全加器的进位中，然后让所有第二个操作数的位取反，即异或1。

溢出检测方法：如果按照第一种溢出方法进行检测，将最高位输出结果与两个最高位输入进行检测，看是否满足正正得负或者负负得正的情况。如果按照第二种溢出方法检测则更加简单，只需要对最高位全加器的进位输出与次高位全加器的进位输出异或即可。

缺点：串行进位，计算时间长。优化：并行计算，首先求出每一位进位的条件，然后用门电路连接输入与输出，这样能够实现仅依靠操作数输入而不需要前一位的进位就可以判断某一位是否会产生进位。

3.3 定点乘法运算

3.3.1 原码一位乘法

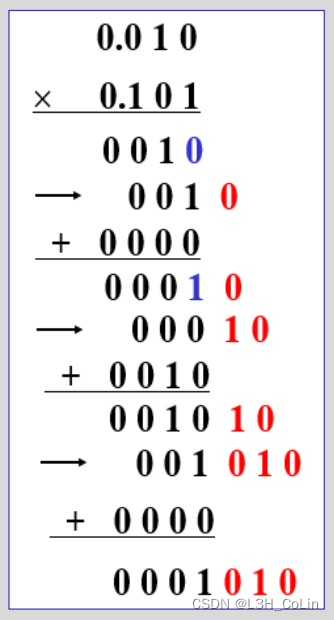
二进制乘法的手工计算与十进制的乘法类似，都使用竖式计算。
缺点：

• 需要多个输入的全加器
  • 解决方式：基于全加器循环累加0或被乘数
• 需要长度足够的结果寄存器
  • 解决方式：从部分积和乘数寄存器中获取结果
• 对应乘数的不同位，部分积的左移次数不同，且整个过程中总的移位次数较多。
  • 解决方式：右移部分积

原码一位乘法流程：

3.3.2 补码一位乘法

$$[x×y]_补=[x]_补\times 0.y_1y_2...y_n-[x]_补\times y_0\\ =[x]_补\times\sum_{i=0}^n(y_{i+1}-y_i)2^{-i}$$

由上面公式可推出运算规则：

• 如果y_n+1=y_n，部分积加0，算数右移1位。
• 如果y_ny_n+1=01，部分积加[x]_补，算数右移1位。
• 如果y_ny_n+1=10，部分积加[-x]_补，算数右移1位。
• 重复进行n+1步，最后一步不右移。

注意补码乘数在运算开始时符号位为1位，且后面要补一个0。

3.4 定点除法计算

3.4.1 原码一位除法

原码恢复余数除法

每一次需要尝试，如果不够减还需要重新加回去。

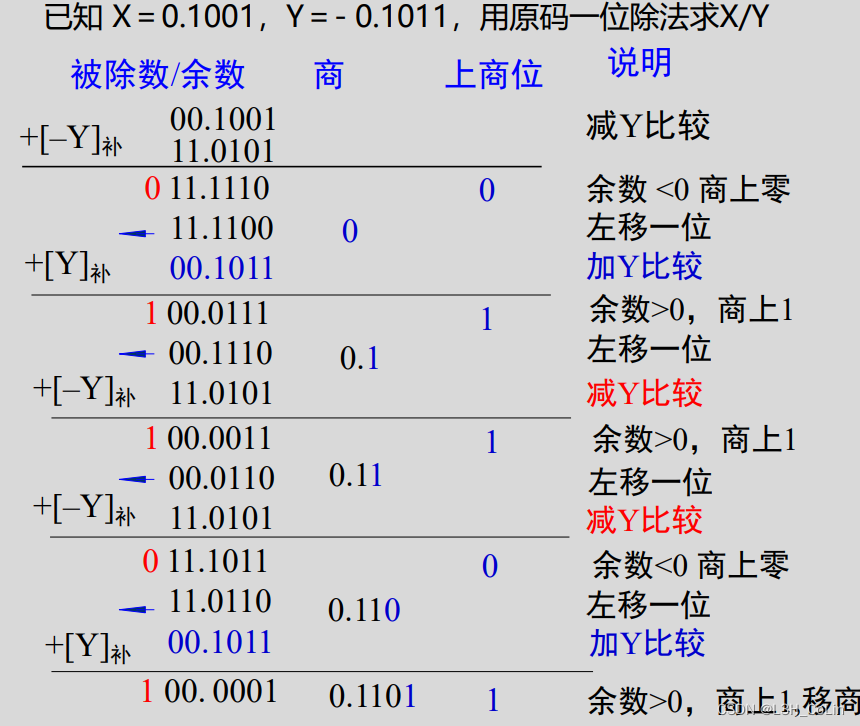
原码不恢复余数除法

当不够减时，下一次计算则是左移之后加，即加减交替。不够减或不够加商都上0，否则都上1。

3.5 浮点运算

3.5.1 浮点加减法计算

规格化浮点数

将一个浮点数按照指定的格式进行转换，规格化浮点数的尾数形式为00.1…或11.0…。如果是00.0…或11.1…这个形式，则需要进行左移，将尾数向左移动，每一次移动阶码-1，直到尾数为规范形式。当尾数为01或10开头时需要右移，阶码+1。

浮点数加减

• 对阶：求出两个数的阶码的差，然后右移阶码小的数的尾数并增加其阶码直到二者阶码相等。
• 尾数加减
• 结果规格化
• 右移舍入规则：
  • 0舍1入：如果右移出去的是1，则在最低位加1
  • 恒置1：只要1被移出就将最后一位置为1。
• 溢出处理：当阶码的尾数为01开头说明为尾数上溢，为10开头说明为下溢。