编译原理——第4章(2)

题型总结

1. LL(1)文法分析

该类题型主要包括左递归消除、回溯消除、构建预测分析表、还原递归分析过程、还原预测分析过程等。

例-1（课后习题4-3改）设文法$G[S]$：
$S\rightarrow A$
$A\rightarrow B|AiB$
$B\rightarrow C|B+C$
$C\rightarrow )A*|($

(1) 将文法$G[S]$改写为LL(1)文法。

分析：改写LL(1)文法第一步——消除左递归。

首先发现$A\rightarrow AiB$存在左递归，于是将第2条规则改写为：
$A\rightarrow BA'$
$A'\rightarrow iBA'|\varepsilon$（注意这里不能没有$\varepsilon$！）

然后第3条规则显然也有左递归，继续改写：
$B\rightarrow CB'$
$B'\rightarrow +CB'|\varepsilon$

至此左递归消除完成。文法变为：
$S\rightarrow A$
$A\rightarrow BA'$
$A'\rightarrow iBA'|\varepsilon$
$B\rightarrow CB'$
$B'\rightarrow +CB'|\varepsilon$
$C\rightarrow )A*|($

下面查看这其中是否有回溯。对于左部相同的两条规则：

• $A'\rightarrow iBA'|\varepsilon$，其$\operatorname{SELECT}$集分别为$\{i\}$和$\{*,$ $ $\}$，无交集（注意这里的$是由$\operatorname{FOLLOW}$集产生的，如果一个非终结符后面可以不跟任何终结符，那么就需要将符号串的结束符$包含到$\operatorname{SELECT}$集中。）
• $B'\rightarrow +CB'|\varepsilon$，其$\operatorname{SELECT}$集分别为$\{+\}$和$\{i,*,$ $ $\}$，无交集。
• $C\rightarrow )A*|($，其$\operatorname{SELECT}$集分别为$\{)\}$和$\{(\}$，无交集。

注意这里的$\operatorname{FOLLOW}$集计算过程。盲目去找很容易漏掉几个。找$\operatorname{FOLLOW}$集不应该只是去找某一个非终结符的$\operatorname{FOLLOW}$集，而是应该从头到尾将所有非终结符的$\operatorname{FOLLOW}$集全部找到，因为一些非终结符的$\operatorname{FOLLOW}$集可以直接加载其他非终结符的$\operatorname{FOLLOW}$集之中。
对于上例中的文法。我们来使用规范化的方式寻找$\operatorname{FOLLOW}$集：

• 对于$S$，其为开始符号，后面本来就可以不跟什么符号，因此$ $\in\operatorname{FOLLOW}(S)$。又有$S\rightarrow A$，因此$A$的$\operatorname{FOLLOW}$集中一定包含$S$的$\operatorname{FOLLOW}$集中的所有元素。注意此时我们并不确定$S$的$\operatorname{FOLLOW}$集中是否只有一个$。

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{$ $ $\}$

• 对于文法$A\rightarrow BA'$，有$\operatorname{FOLLOW}(A)\subseteq\operatorname{FOLLOW}(A')$，$\operatorname{FIRST}(A')\subseteq\operatorname{FOLLOW}(B)$，其中$\operatorname{FIRST}(A')=\{i,\varepsilon\}$

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{$ $ $\}$
$A'$	$\{$ $ $\}$
$B$	$\{i,$ $ $\}$

• 对于文法$B\rightarrow CB'$，有$\operatorname{FIRST}(B')\subseteq\operatorname{FOLLOW}(C)$，其中$\operatorname{FIRST}(B')=\{+,\varepsilon\}$，且有$\operatorname{FOLLOW}(B)\subseteq\operatorname{FOLLOW}(B')$，$\operatorname{FOLLOW}(B')\in\operatorname{FOLLOW}(C)$。

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{$ $ $\}$
$A'$	$\{$ $ $\}$
$B$	$\{i,$ $ $\}$
$B'$	$\{i,$ $ $\}$
$C$	$\{+,$ $ $\}$

• 对于文法$C\rightarrow )A*|($，有$*\in\operatorname{FOLLOW}(A)$。

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{*,$ $ $\}$
$A'$	$\{$ $ $\}$
$B$	$\{i,$ $ $\}$
$B'$	$\{i,$ $ $\}$
$C$	$\{+,$ $ $\}$

• 扩充被$A$影响的$\operatorname{FOLLOW}$集：

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{*,$ $ $\}$
$A'$	$\{*,$ $ $\}$
$B$	$\{i,$ $ $\}$
$B'$	$\{i,$ $ $\}$
$C$	$\{+,$ $ $\}$

• 对于文法$A'\rightarrow iBA'|\varepsilon$，有$\operatorname{FOLLOW}(A')\in\operatorname{FOLLOW}(B)$。

	FOLLOW集
$S$	$\{$ $ $\}$
$A$	$\{*,$ $ $\}$
$A'$	$\{*,$ $ $\}$
$B$	$\{i,*,$ $ $\}$
$B'$	$\{i,*,$ $ $\}$
$C$	$\{i,*,+,$ $ $\}$

故不存在回溯问题。

最终修改完成的文法为：
$S\rightarrow A$
$A\rightarrow BA'$
$A'\rightarrow iBA'|\varepsilon$
$B\rightarrow CB'$
$B'\rightarrow +CB'|\varepsilon$
$C\rightarrow )A*|($

(2) 求经过改写后的每个非终结符的$\operatorname{FIRST}$集和$\operatorname{FOLLOW}$集，以及每一条规则的$\operatorname{SELECT}$集。

解：$\operatorname{FIRST}$集和$\operatorname{FOLLOW}$集如下：

	FIRST集	FOLLOW集
$S$	$\{),(\}$	$\{$ $ $\}$
$A$	$\{),(\}$	$\{*,$ $ $\}$
$A'$	$\{i,\varepsilon\}$	$\{*,$ $ $\}$
$B$	$\{),(\}$	$\{i,*,$ $ $\}$
$B'$	$\{+,\varepsilon\}$	$\{i,*,$ $ $\}$
$C$	$\{),(\}$	$\{i,*,+,$ $ $\}$

$\operatorname{SELECT}$集如下：

	SELECT集
$S\rightarrow A$	$\{),(\}$
$A\rightarrow BA'$	$\{),(\}$
$A'\rightarrow iBA'$	$\{i\}$
$A'\rightarrow\varepsilon$	$\{*,$ $ $\}$
$B\rightarrow CB'$	$\{),(\}$
$B'\rightarrow +CB'$	$\{+\}$
$B'\rightarrow \varepsilon$	$\{i,*,$ $ $\}$
$C\rightarrow )A*$	$\{)\}$
$C\rightarrow ($	$\{(\}$

(3) 写出该文法的递归下降分析程序的$A'$函数、$B'$函数和$C$函数：

解：

A'(){
	if(sym == 'i'){
		scanner();		// 输入符号串读位置前移一位
		B();
		A'();
	}else if(sym != '*' && sym != '$')
		error();
	else
		scanner();
}

B'(){
	if(sym == '+'){
		C();
		B'();
	}else if(sym != 'i' && sym != '*' && sym != '$')
		error();
}

C(){
	if(sym == '('){
		scanner();
		A();
		scanner();
		if(sym != '*')
			error();
	}else if(sym != ')')
		error();
	scanner();
}

递归下降分析函数需要保证：在任何一个非终结符识别函数刚刚开始执行时，读位置始终指向该非终结符应该识别的第一个字符。因此调整指针的操作应该在上一级函数中实现，这也是$A$函数和$C$函数最后一句scanner()的含义。

(4) 画出预测分析图。

解：可以根据$\operatorname{SELECT}$集直接画出预测分析图：

	(	)	*	+	i	$
$S$	$S\rightarrow A$	$S\rightarrow A$
$A$	$A\rightarrow BA'$	$A\rightarrow BA'$
$A'$			$A'\rightarrow\varepsilon$		$A'\rightarrow iBA'$	$A'\rightarrow\varepsilon$
$B$	$B\rightarrow CB'$	$B\rightarrow CB'$
$B'$			$B'\rightarrow \varepsilon$	$B'\rightarrow +CB'$	$B'\rightarrow \varepsilon$	$B'\rightarrow \varepsilon$
$C$	$C\rightarrow ($	$C\rightarrow )A*$

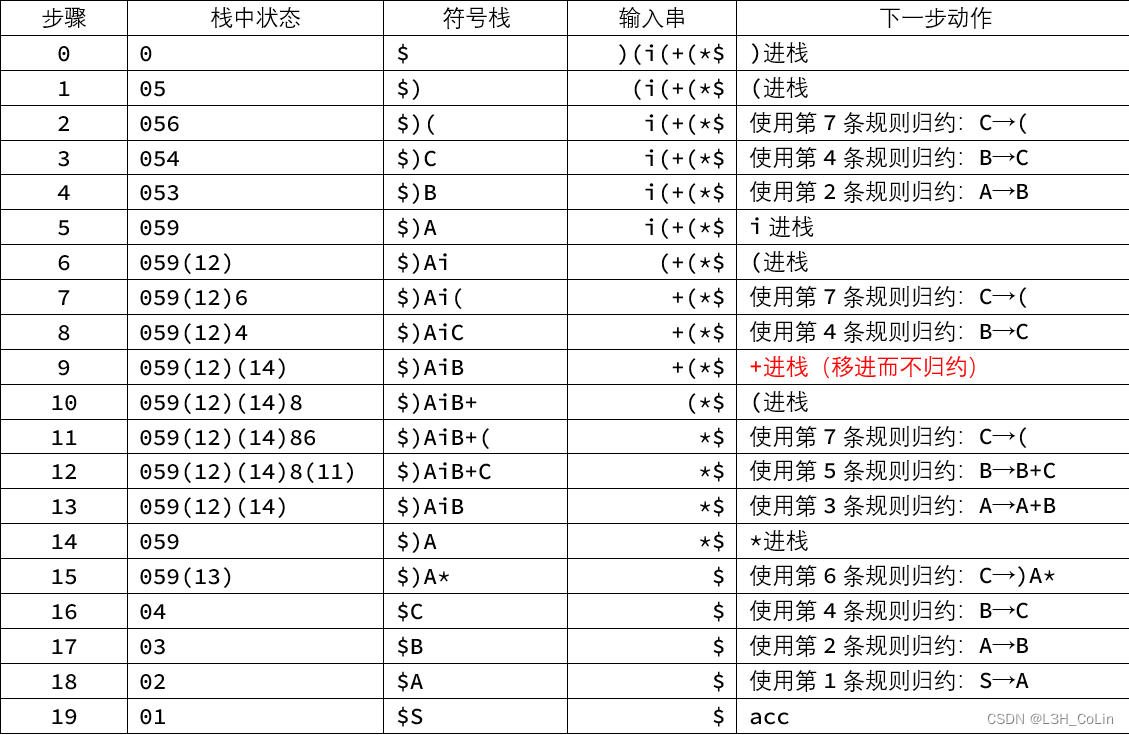
(5) 使用上面的预测分析图分析输入串)(i(+(*。

解：画图——

分析栈	输入串	所用规则
$	)(i(+(*$
$A	)(i(+(*$	$S\rightarrow A$
$A'B	)(i(+(*$	$A\rightarrow BA'$
$A'B'C	)(i(+(*$	$B\rightarrow CB'$
$A'B'*A)	)(i(+(*$	$C\rightarrow )A*$
$A'B'*A'B	(i(+(*$	$A\rightarrow BA'$
$A'B'*A'B'C	(i(+(*$	$B\rightarrow CB'$
$A'B'*A'B'(	(i(+(*$	$C\rightarrow ($
$A'B'*A'B'	i(+(*$
$A'B'*A'	i(+(*$	$B'\rightarrow \varepsilon$
$A'B'*A'Bi	i(+(*$	$A'\rightarrow iBA'$
$A'B'*A'B	(+(*$
$A'B'*A'B'C	(+(*$	$B\rightarrow CB'$
$A'B'*A'B'(	(+(*$	$C\rightarrow ($
$A'B'*A'B'	+(*$
$A'B'*A'B'C+	+(*$	$B'\rightarrow +CB'$
$A'B'*A'B'C	(*$
$A'B'*A'B'(	(*$	$C\rightarrow ($
$A'B'*A'B'	*$
$A'B'*A'	*$	$B'\rightarrow \varepsilon$
$A'B'*	*$	$A'\rightarrow\varepsilon$
$A'B'	$
$A'	$	$B'\rightarrow \varepsilon$
$	$	$A'\rightarrow\varepsilon$

成功。

上面的分析流程：如果栈中最上面一个是非终结符，下一步就要根据输入串最前面的字符选择候选式。如果栈中最上面一个是终结符，就和输入串最前面的字符比较，如果相等就相消，如果不等就输出错误。

2. OG文法分析

OG文法没有讲完，后面的素短语等内容没有要求，因此只需要掌握两个集合的求解以及算符优先表的构建即可。

例-2：对于例-1中的文法，求所有非终结符的$\operatorname{FIRSTVT}$集和$\operatorname{LASTVT}$集，并画出算符优先表。

$S\rightarrow A$
$A\rightarrow B|AiB$
$B\rightarrow C|B+C$
$C\rightarrow )A*|($

分析：按照构建两个集合的方法求出所有非终结符的$\operatorname{FIRSTVT}$集和$\operatorname{LASTVT}$集：

	FIRSTVT	LASTVT
$S$	$\{i,(,),+\}$	$\{i,*,(,+\}$
$A$	$\{i,(,),+\}$	$\{i,*,(,+\}$
$B$	$\{(,),+\}$	$\{*,(,+\}$
$C$	$\{(,)\}$	$\{*,(\}$

构建算符优先表：

	i	(	)	+	*	$
i	$\gtrdot$	$\lessdot$	$\lessdot$	$\lessdot$	$\gtrdot$	$\gtrdot$
(	$\gtrdot$			$\gtrdot$	$\gtrdot$	$\gtrdot$
)	$\gtrdot,\lessdot$	$\lessdot$	$\lessdot$	$\lessdot$	$\eqcirc$
+	$\gtrdot$	$\lessdot$	$\lessdot$	$\gtrdot$	$\gtrdot$	$\gtrdot$
*				$\gtrdot$	$\gtrdot$	$\gtrdot$
$	$\lessdot$	$\lessdot$	$\lessdot$	$\lessdot$		$\eqcirc$

3. LR(0)文法

该部分包含LR(0)文法的分析表、活前缀DFA的构建。

例-3：画出例-1中文法的规范句型活前缀DFA以及LR(0)分析表，如果有冲突说明冲突来源，没有冲突说明理由。

$S\rightarrow A$
$A\rightarrow B|AiB$
$B\rightarrow C|B+C$
$C\rightarrow )A*|($

分析：首先拓广，加一条规则：
$S'\rightarrow S$
$S\rightarrow A$
$A\rightarrow B|AiB$
$B\rightarrow C|B+C$
$C\rightarrow )A*|($

然后递归地构建DFA：

• 求出$\operatorname{CLOSURE}(S'\rightarrow\cdot S)=\{S'\rightarrow\cdot S,S\rightarrow\cdot A,A\rightarrow\cdot B,A\rightarrow\cdot AiB,B\rightarrow\cdot C,B\rightarrow\cdot B+C,C\rightarrow\cdot)A*,C\rightarrow\cdot(\}$，作为项目集$I_0$。
• 求出$\operatorname{GOTO}(I_0,S)=\operatorname{CLOSURE}(\{S'\rightarrow S\cdot\})=\{S'\rightarrow S\cdot\}$，作为项目集$I_1$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_0,A)=\operatorname{CLOSURE}(\{S\rightarrow A\cdot,A\rightarrow A\cdot iB\})=\{S\rightarrow A\cdot,A\rightarrow A\cdot iB\}$，作为项目集$I_2$。
• 求出$\operatorname{GOTO}(I_0,B)=\operatorname{CLOSURE}\{A\rightarrow B\cdot,B\rightarrow B\cdot +C\}=\{A\rightarrow B\cdot,B\rightarrow B\cdot +C\}$，作为项目集$I_3$。
• 求出$\operatorname{GOTO}(I_0,C)=\operatorname{CLOSURE}\{B\rightarrow C\cdot\}=\{B\rightarrow C\cdot\}$，作为项目集$I_4$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_0,")")=\operatorname{CLOSURE}\{C\rightarrow )\cdot A*\}=\{C\rightarrow )\cdot A*,A\rightarrow\cdot B,A\rightarrow\cdot AiB,B\rightarrow\cdot C,B\rightarrow\cdot B+C,C\rightarrow\cdot)A*,C\rightarrow\cdot(\}$，作为项目集$I_5$。
• 求出$\operatorname{GOTO}(I_0,"(")=\operatorname{CLOSURE}\{C\rightarrow (\cdot\}=\{C\rightarrow (\cdot\}$，作为项目集$I_6$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_2,i)=\operatorname{CLOSURE}(\{A\rightarrow Ai\cdot B\})=\{A\rightarrow Ai\cdot B\}$，作为项目集$I_7$。
• 求出$\operatorname{GOTO}(I_3,+)=\operatorname{CLOSURE}(\{B\rightarrow B+\cdot C\})=\{B\rightarrow B+\cdot C,C\rightarrow\cdot)A*,C\rightarrow\cdot(\}$，作为项目集$I_8$。
• 求出$\operatorname{GOTO}(I_5, A)=\operatorname{CLOSURE}(\{C\rightarrow)A\cdot*,A\rightarrow A\cdot iB\})=\{C\rightarrow)A\cdot*,A\rightarrow A\cdot iB\}$，作为项目集$I_9$。
• 求出$\operatorname{GOTO}(I_5, B)=\operatorname{CLOSURE}(\{A\rightarrow B\cdot, B\rightarrow B\cdot+C\})=I_3$。
• 求出$\operatorname{GOTO}(I_5, C)=\operatorname{CLOSURE}\{B\rightarrow C\cdot\}=I_4$。
• 求出$\operatorname{GOTO}(I_5, "(")=\operatorname{CLOSURE}(\{C\rightarrow (\cdot\})=I_6$。
• 求出$\operatorname{GOTO}(I_5,")")=\operatorname{CLOSURE}(\{C\rightarrow )\cdot A*\})=I_5$。
• 求出$\operatorname{GOTO}(I_7, B)=\operatorname{CLOSURE}(\{A\rightarrow AiB\cdot\})=\{A\rightarrow AiB\cdot\}$，作为项目集$I_{10}$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_8, C)=\operatorname{CLOSURE}(\{B\rightarrow B+C\cdot\})=\{B\rightarrow B+C\cdot\}$，作为项目集$I_{11}$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_8, ")")=\operatorname{CLOSURE}(\{C\rightarrow)\cdot A*\})=I_5$。
• 求出$\operatorname{GOTO}(I_8,"(")=\operatorname{CLOSURE}\{C\rightarrow (\cdot\}=I_6$。
• 求出$\operatorname{GOTO}(I_9, i)=\operatorname{CLOSURE}(\{A\rightarrow Ai\cdot B\})=\{A\rightarrow Ai\cdot B,B\rightarrow\cdot C,B\rightarrow\cdot B+C,C\rightarrow\cdot)A*,C\rightarrow\cdot(\}$，作为项目集$I_{12}$。
• 求出$\operatorname{GOTO}(I_9, *)=\operatorname{CLOSURE}(\{C\rightarrow)A*\cdot\})=\{C\rightarrow)A*\cdot\}$，作为项目集$I_{13}$，其没有$\operatorname{GOTO}$函数。
• 求出$\operatorname{GOTO}(I_{12},B)=\{A\rightarrow AiB\cdot,B\rightarrow B\cdot+C\}$，作为项目集$I_{14}$，有$\operatorname{GOTO}(I_{14},+)=I_8$。
• 求出$\operatorname{GOTO}(I_{12},C)=\{B\rightarrow C\cdot\}=I_4$。
• 求出$\operatorname{GOTO}(I_{12},")")=I_5$。
• 求出$\operatorname{GOTO}(I_{12},"(")=I_6$。

由上面的推导画出DFA（图略，太复杂）
根据上面的推导画出分析表如下：

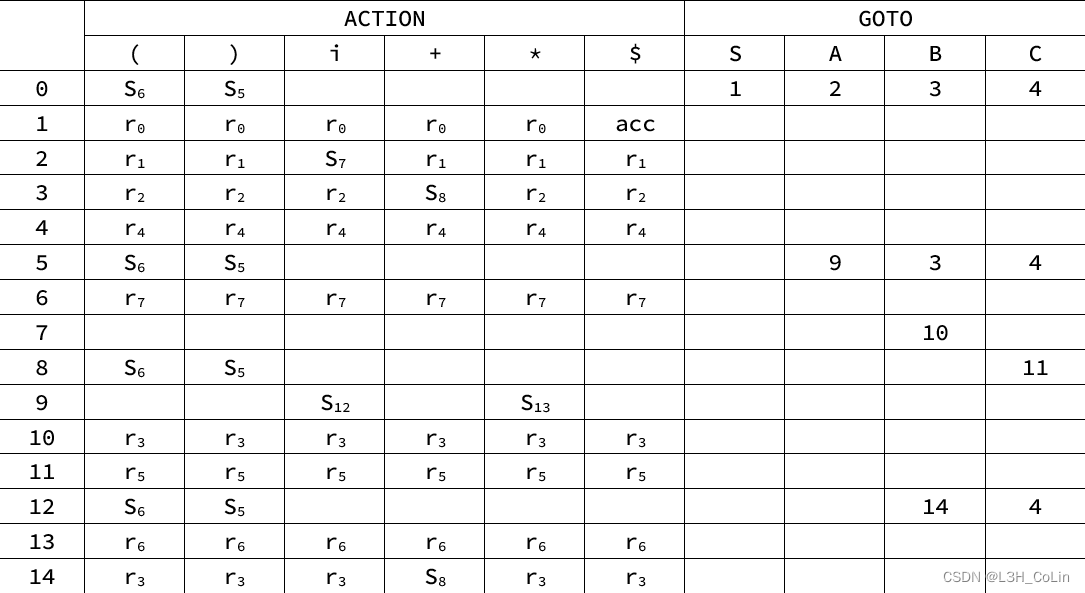
可以看见其中有多处移进-归约冲突。

4. SLR(1)文法

例-4：使用SLR(1)文法尝试改写上一题的分析表，说明改写后是否存在冲突。如果不存在，试分析符号串)(i(+(*

分析：上图中一共有3处移进-规约冲突，下面逐一进行处理：

• 对于状态2移入符号$i$，状态2的两个LR(0)项目中只有$\{A\rightarrow A\cdot iB\}$可以接受符号$i$，而另一个状态$\{S\rightarrow A\cdot\}$无法接收符号$i$（$\operatorname{FOLLOW}$集中不包含$i$）。因此此处冲突可以解决。
• 对于状态3移入符号$+$，状态3的两个LR(0)项目中只有$\{B\rightarrow B\cdot +C\}$可以接受，而另一个无法接受。因此此处状态可以解决。
• 对于状态14移入符号$+$，状态14的两个LR(0)项目中只有$\{B\rightarrow B\cdot +C\}$可以接受，而另一个无法接受。因此此处状态可以解决。

至此冲突已经完全解决，可以进行分析了。分析过程如下：